Расчёт активных фильтров. Онлайн калькулятор.
И начнём мы с активных фильтров нижних частот (ФНЧ) и фильтров верхних частот (ФВЧ) 2-го и 3-го порядков имени товарищей Бесселя, Баттерворта и Пафнутия нашего Чебышева.
Эко нас понесло! Почему бы не удовлетвориться одним учёным мужем? К примеру, привычный с детства Баттерворт совсем не плох, к тому же широко известен в узких кругах.
Согласен, с какой стороны не возьми, Баттерворт — хорошая штука. Тут тебе и максимально гладкая АЧХ на частотах полосы пропускания, и
приличный спад характеристики в полосе подавления, однако…
Если на первый план выдвигается линейность фазо-частотной характеристики в полосе пропускания фильтра (например, в аудио-кроссоверах),
то пальма первенства в АЧХ-строении переходит к обратному многочлену профессора Фридриха Вильгельма Бесселя, ну а если ФЧХ нам
до фени, а в приоритете максимально крутой спад характеристики на частотах полосы подавления, то как ни крути, придётся с головой
окунуться в полиномы Пафнутия Львовича Чебышёва.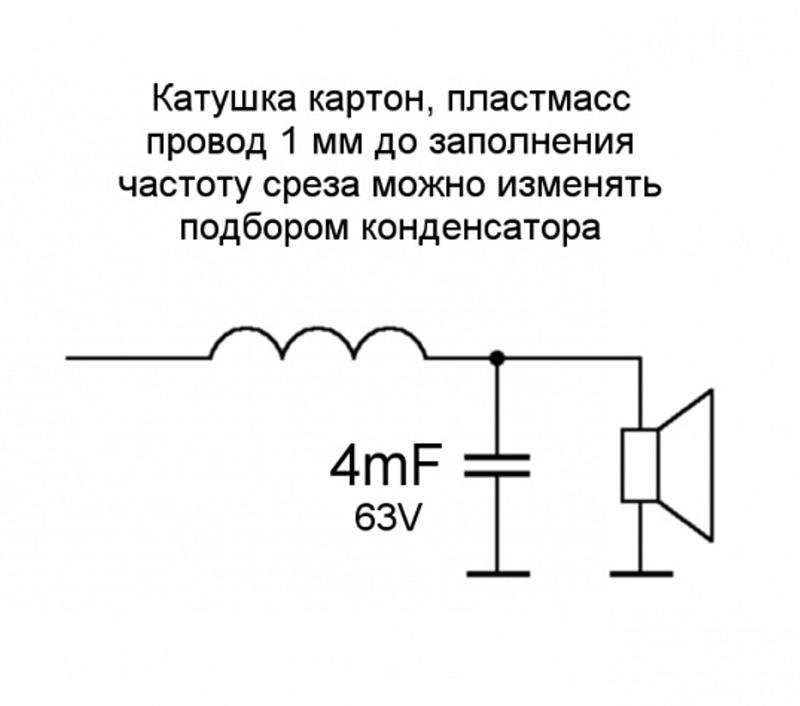
Фильтры построим на основе повторителей, они просты в расчётах, к тому же легко могут быть реализованы не только на операционных усилителях, но и на транзисторах.
А желающим спроектировать активный фильтр нижних частот 3-6-го порядка с перестраиваемой частотой среза, следует посетить страницу ссылка на страницу .
Рис.1
На Рис.1 приведены схемы активных фильтров нижних частот (ФНЧ) 2-го и 3-го порядка на ОУ и, для примера, реализация фильтра на биполярном транзисторе, отличающаяся от схем на операционниках только наличием двух резисторов, задающих необходимое напряжение смещения на базе.
Крутизна спада АЧХ этих фильтров в полосе подавления для Бесселя — около 5 дБ/октаву на каждый порядок фильтра, для
Баттерворта — 6 дБ/октаву и около 8 дБ/октаву для Чебышёва.
Коэффициент передачи в полосе пропускания К=1, а номиналы рассчитываются исходя из формул:
C1=КС1/(2π*F*R)   C2=КС2/(2π*F*R)   C3=КС3/(2π*F*R), где коэффициенты
КС1, КС2 и КС3 зависят как от порядка фильтра, так и от его принадлежности к той или иной фамилии.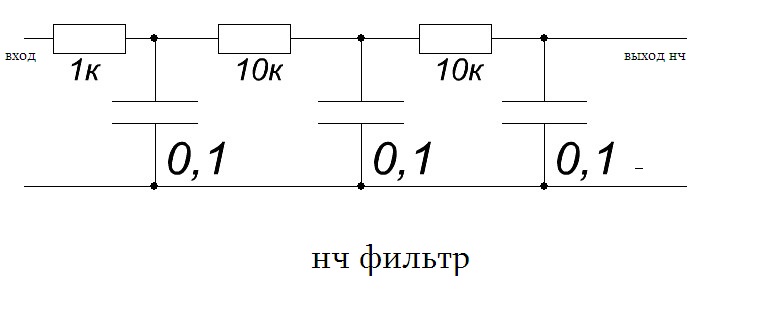
К примеру для фильтров Баттерворта 2-го порядка КС1=1,114, КС2=0,707, а для фильтров Баттерворта 3-го порядка КС1=1,393, КС2=3,549, КС3=0,202.
Критерии выбора величины сопротивления R, такие же, как и в пассивных фильтрах, она должна быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного сопротивления ОУ или ЭП (на практике 1-100 кОм).
РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНЫХ ФНЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА
Плавно переходим к активным фильтрам верхних частот (ФВЧ) 2-го и 3-го порядка на ОУ (Рис.2). В транзисторной реализации резисторы, задающие напряжение смещения на базе, уже участвуют в формировании необходимой АЧХ фильтра, поэтому значение Rб1 ll Rб2 должно равняться значению резистора R2 в ФВЧ 2-го порядка, либо R3 в ФВЧ 3-го порядка.
Рис.2
Номиналы элементов рассчитываются исходя из следующих формул:
R1=КR1/(2π*F*C) R2=КR2/(2π*F*C) R3=КR3/(2π*F*C)
Rrб1llRrб2=R2 для фильтров 2-го порядка, либо Rrб1llRrб2=R3 для 3-го.
И опять же, изначально надо определиться с номиналом R1, исходя из принципов, описанных в предыдущих схемах.
ТАБЛИЦА ДЛЯ РАСЧЁТА АКТИВНЫХ ФВЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА
И наконец, мы подобрались к схеме полосового активного фильтра.
Здесь всё несколько сложнее, поскольку, при расчёте фильтра, помимо значения центральной частоты, нам не стоит забывать
и про такие немаловажные вещи, как коэффициент передачи фильтра в полосе пропускания, да и собственно ширину самой полосы
пропускания.
Формулы, для расчёта элементов:
C1=C2=C
R1=Q/(2πF*Kп*C)
R2=Q/((2πF*C*(2Q²-Kп))
R3=2Q/(2πF*C)
Q=F/Bпр, где
Q-добротность фильтра,
Впр-полоса пропускания по уровню -3дБ,
F-центральная частота фильтра,
Кп-коэффициент передачи фильтра в полосе пропускания.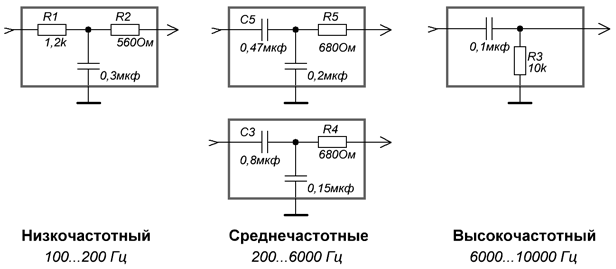
Рис.3
В фильтре, приведённом на рисунке, не стоит слишком усердствовать с высокими значениями добротности и коэффициента передачи. Как показывает практика, и тот и другой параметр следует ограничить сверху на уровне 5-6 единиц.
Как всегда, начинаем с выбора номинала резистора R1, который как минимум в 10 раз должен быть выше выходного импеданса предыдущего каскада.
РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНОГО ПЛОСОВОГО ФИЛЬТРА 2-го ПОРЯДКА
ВНИМАНИЕ!!! Для правильной работы этого фильтра должно соблюдаться условие К<2*Q². При несоблюдении этого условия, значение R2 в таблице примет отрицательное значение.
А что делать, если полученные значения элементов не попадают в стандартную сетку?
Не беда, нарисуем ещё одну таблицу, но до этого надо поиграться коэффициентом передачи фильтра в небольших пределах (например,
сделать не 1,5, а 1,45, или 1,55) до достижения значения R3 величины, попадающей в сетку.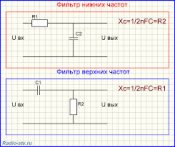
Предположим, нам надо рассчитать фильтры для 10-полосного эквалайзера.
Фильтры у нас получаются октавные, стандартное значение добротности для них Q=1,41.
R1 выберем номиналом 30кОм, Кпер = 1,5. Произведём расчёт для частоты 1000 Гц.
Подставив эти цифры в верхнюю таблицу, получаем С=4987пФ, R2=18,173кОм, R3=90кОм.
Итак, подставляем в нижнюю таблицу R1=30кОм, R3=91кОм, R2=18кОм, стандартное значение ёмкости С=5100пФ и естественным образом видим, что значение резонансной частоты у нас съехало до 975Гц.
Но у нас было с собой, а именно замечательное сопротивление R2, которое никак не влияет на Кпер, и весьма скромно — на добротность.
Покрутив номинал этого резистора, получаем — 16,7кОм, центральную частоту — 999Гц и добротность — 1.46. Всё, расчёт фильтра — завершён.
ЕЩЁ ТАБЛИЦА ДЛЯ АКТИВНОГО ПОЛОСОВОГО ФИЛЬТРА
Для желающих рассчитать параметры и элементы многополосных графических эквалайзеров следует посетить страницу ссылка на страницу , а на следующей странице мы рассмотрим универсальный перестраиваемый активный фильтр с регулировкой частоты и добротности.
Практическое применение операционных усилителей.Часть вторая.
РадиоКот >Статьи >Практическое применение операционных усилителей.Часть вторая.
Итак, в первой части мы рассмотрели схемы включения ОУ в качестве усилителей, в этой части рассмотрим включения ОУ в качестве фильтров.
Фильтр Высоких Частот (ФВЧ, High-Pass — как угодно)
Требуется он для отсекания сигнала, частота которого ниже определенного порога, который называется, кстати, частотой среза.
Простейший ФВЧ выглядит так:
Это фильтр первого порядка с ослаблением ненужного сигнала — крутизной — 6дБ на октаву. Определить частоту среза можно, рассчитывая реактивное сопротивление конденсатора. Когда оно станет равным сопротивлению резистора, включенного последовательно с конденсатором — это будет самое то.
Формула следующая:
Где F — частота в Герцах, C — емкость в Фарадах, Ec — сопротивление в Омах.
Если крутизна фильтра первого порядка кажется недостаточной, можно справить фильтр второго порядка — с крутизной 12 дБ на октаву как показано на рисунке.
Это — так называемый, фильтр Баттерворта.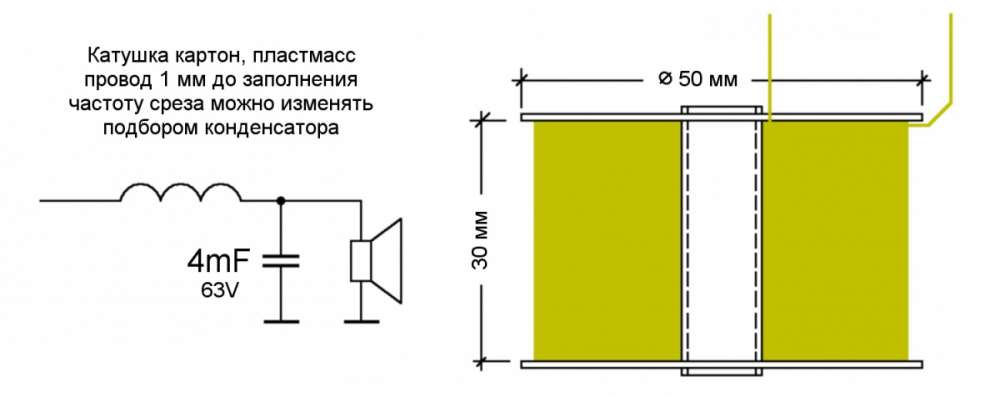
Чтобы посчитать его граничную частоту можно воспользоваться следующими соотношениями:
R1=R2; С1=2С2;
При выборе резисторов надо учесть, что их номиналы должны лежать в пределах 10-100 кОм, поскольку выходное сопротивление фильтра растет вместе с частотой и если номиналы резисторов выходят за вышеуказанные рамки это может сказаться на работе фильтра. Отрицательно, разумеется — иначе зачем предупреждать?
Фильтр Низких Частот (ФНЧ, Low-Pass — как угодно)
Работа этого фильтра прямо противоположна предыдущему — он отрезает сигнал, частота которого выше частоты среза.
В принципе, все то же самое, что и в предыдущем случае, только конденсатор включается не последовательно с резистором, а параллельно ему.
Первая схема — неинвертирующее включение, вторая — инвертирующее. Частота среза считается ровно таким же способом, как и в случае ФВЧ.
Ну и схема фильтра второго порядка — того же самого гражданина Баттерворта.
Опять же — считается все точно так же, как было описано выше.
Полосовой Фильтр (Band-Pass)
Полосовой фильтр применяется в тех случаях, когда необходимо выделить некую полосу частот из всего спектра. Например, в спектроанализаторах или вроде того.
Формулы расчета приводить тут не буду — дюже они забористые. Для расчета полосовых фильтром советую воспользоваться замечательной программой — Filter Wiz Pro от Schematica Software. Впрочем, ей так же можно воспользоваться и для расчетов любых других фильтров.
Фильтр-пробка (Notch Filter)
Если вам нужно ослабить (практически до нуля) некую выбранную частоту, то это фильтр как раз для вас.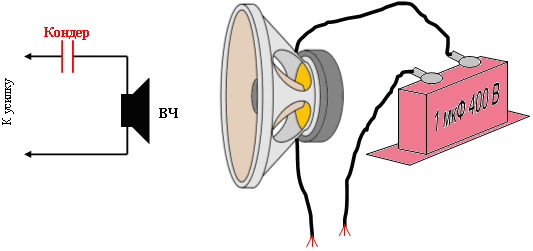
Формула расчета вот такая:
где R=R3=R4, C=C1=C2;
При построении этого фильтра очень важна точность номиналов компонентов — от этого зависит степень «убивания» выбранной частоты. Так, при применении резисторов и конденсаторов с допуском 1%, можно получить ослабление частоты до 45дБ, хотя, теоретически, можно добиться и 60дБ.
Например, если вы хотите грохнуть ненавистную всем частоту 50Гц, то берем следующие номиналы: R1=R2=10кОм, R3=R4=68кОм, С1=С2=47нФ.
Фильтр-пробка с двойным Т-мостом.
С помощью этого фильтра можно не только ослаблять выбранную частот, но и регулировать степень её ослабления переменным резистором R4. Формула расчета номиналов такая же, как и в предыдущем случае.
С фильтрами все, в следующей части еще кое-что интересное.
Вопросы, как обычно, складываем тут.
Как вам эта статья? | Заработало ли это устройство у вас? |
Как рассчитать фильтр для акустики
Трёхполосные акустические системы, состоящие из трёх динамиков, являются самым удачным решением для высококачественного звуковоспроизведения.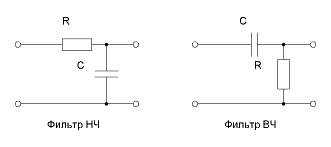 В них используются три типа звуковых головок. Они отличаются по размеру, конструктивным особенностям и полосе воспроизводимых частот. Для разделения всего частотного диапазона выдаваемого усилителем низкой частоты используются полосовые фильтры-кроссоверы. В них используются конденсаторы дроссели и, реже, резисторы.
В них используются три типа звуковых головок. Они отличаются по размеру, конструктивным особенностям и полосе воспроизводимых частот. Для разделения всего частотного диапазона выдаваемого усилителем низкой частоты используются полосовые фильтры-кроссоверы. В них используются конденсаторы дроссели и, реже, резисторы.
Сделать своими руками фильтр для динамика НЧ очень просто.Основным элементом устройства является индуктивность или дроссель. Катушка включается последовательно с низкочастотным динамиком.
Фильтр для низкочастотного динамика
Фильтр нижних частот из дросселя и конденсатора большой ёмкости называется схемой Баттерворта второго порядка. Он обеспечивает спад частот выше частоты среза до 12 dBна октаву. Схема работает следующим образом. Индуктивность в LC контуре выполняет функцию переменного резистора. Его сопротивление прямо пропорционально частоте ивозрастает с увеличением диапазона. Поэтому высокие частоты практически не попадают на НЧ динамик.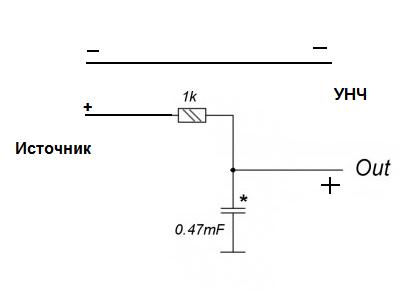 Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Поскольку схема устройства должна хорошо пропускать низкие частоты и обрезать высокие, то конденсаторы такого устройства имеют большую ёмкость.Пассивный фильтр для динамика может быть выполнен по более сложной схеме. Если соединить две схемы Баттерворта последовательно, то получится устройство четвёртого порядка из двух индуктивностей и двух конденсаторов. Оно обеспечивает спад частотной характеристики низкочастотного громкоговорителя в 24 децибела на октаву.
Для того чтобы выровнять частотную характеристику и более точно согласовать схему Баттерворта и динамик, между катушкой индуктивности и конденсатором, включается резистор с небольшим сопротивлением. Для этой цели лучше использовать проволочные резисторы.
Фильтры для динамиков своими руками
Сделать фильтр для динамика совсем не сложно. Он состоит всего из двух элементов – конденсатора и катушки индуктивности. Рассчитать параметры радиоэлементов для пассивной схемы низкой частоты второго порядка проще всего на онлайн калькуляторе. Там можно задать желаемый уровень среза и сопротивление акустической головки. Программа выдаст требуемую ёмкость конденсатора и индуктивность катушки. Например, выбран уровень среза 150 Гц, а сопротивление динамика равно 4 Ом. Калькулятор выдаст следующие значения:
Рассчитать параметры радиоэлементов для пассивной схемы низкой частоты второго порядка проще всего на онлайн калькуляторе. Там можно задать желаемый уровень среза и сопротивление акустической головки. Программа выдаст требуемую ёмкость конденсатора и индуктивность катушки. Например, выбран уровень среза 150 Гц, а сопротивление динамика равно 4 Ом. Калькулятор выдаст следующие значения:
- Ёмкость конденсатора – 187 мкф
- Индуктивность катушки – 6,003 мГн
Требуемую ёмкость можно получить из параллельно соединённых конденсаторов К78-34, которые специально разработаны для работы в акустических системах. Кроме того есть обновлённая линейка конденсаторов аналогичного типа. Это KZKWhiteLine. В качестве недорогих аналогов, радиолюбители часто используют конденсаторы типа МБГО или МБГП.
Катушка индуктивности на 6 мГн наматывается на оправке диаметром 1 см и длиной 6 см. Поскольку катушка не имеет магнитного сердечника в качестве бобины можно использовать цилиндр из любого материала, на который для удобства намотки, нужно сделать щёчки.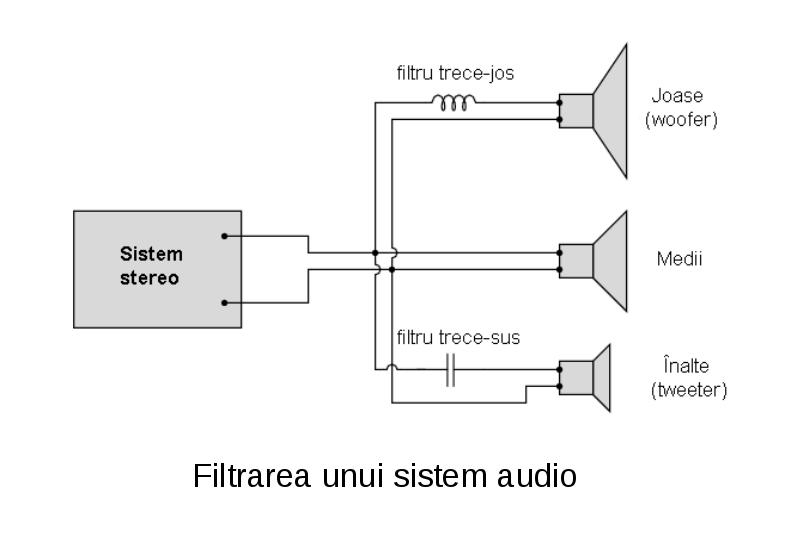 Для намотки используется медный провод типа ПЭЛ диаметром 1 мм. Длина проволоки 84 метра. Намотку нужно делать виток к витку.
Для намотки используется медный провод типа ПЭЛ диаметром 1 мм. Длина проволоки 84 метра. Намотку нужно делать виток к витку.
С целью снижения интермодуляционных искажений при звуковоспроизведении громкоговорители Hi-Fi систем составляют из низкочастотных, среднечастотных и высокочастотных динамических головок. Их подключают к выходам усилителей через разделительные фильтры, представляющие собой комбинации LC фильтров нижних и верхних частот.
Ниже приведена методика расчета трехполосного разделительного фильтра по наиболее распространенной схеме.
Частотная характеристика разделительного фильтра трехполосного громкоговорителя в общем виде показана на рис. 1. Здесь: N – относительный уровень напряжения на звуковых катушках головок: fн и fв – нижняя и верхняя граничные частоты воспроизводимой громкоговорителем полосы; fр1 и fр2 – частоты раздела.
В идеальном случае выходная мощность на частотах раздела должна распределяться поровну между двумя головками. Это условие выполняется, если на частоте раздела относительный уровень напряжения, поступающего на соответствующую головку, снижается на 3 дБ по сравнению с уровнем в средней части ее рабочей полосы частот.
Это условие выполняется, если на частоте раздела относительный уровень напряжения, поступающего на соответствующую головку, снижается на 3 дБ по сравнению с уровнем в средней части ее рабочей полосы частот.
Частоты раздела следует выбирать вне области наибольшей чувствительности уха (1. 3 кГц). При невыполнении этого условия, из-за разности фаз колебаний, излучаемых двумя головками на частоте раздела одновременно, может быть заметно «раздвоение» звука. Первая частота раздела обычно лежит в интервале частот 400. 800 Гц, а вторая – 4. 6 кГц. При этом низкочастотная головка будет воспроизводить частоты в диапазоне fн. fp1. среднечастотная – в диапазоне fp1. fр2 и высокочастотная – в диапазоне fр2. fв.
Один из распространенных вариантов электрической принципиальной схемы трехполосного громкоговорителя приведен на рис. 2. Здесь: B1 – низкочастотная динамическая головка, подключенная к выходу усилителя через фильтр нижних частот L1C1; В2 – среднечастотная головка, соединенная с выходом усилителя через полосовой фильтр, образованный фильтрами верхних частот C2L3 и нижних частот L2C3.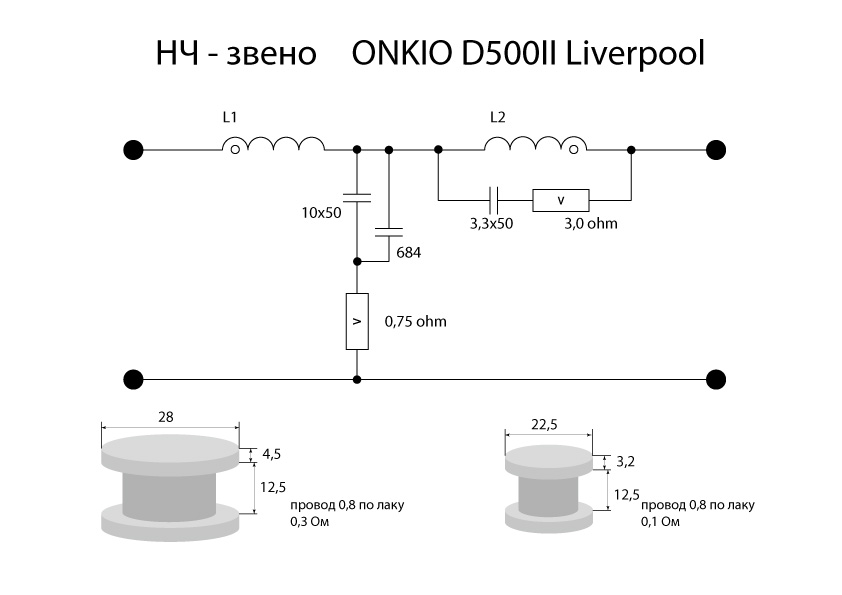 На высокочастотную головку В3 сигнал подается через фильтры верхних частот C2L3 и C4L4.
На высокочастотную головку В3 сигнал подается через фильтры верхних частот C2L3 и C4L4.
Расчет емкостей конденсаторов и индуктивностей катушек производят исходя из номинального сопротивления головок громкоговорителя. Поскольку номинальные сопротивления головок и номинальные емкости конденсаторов образуют ряды дискретных значений, а частоты раздела могут варьироваться в широких пределах, то расчет удобно производить в такой последовательности. Задавшись номинальным сопротивлением головок, подбирают емкости конденсаторов из ряда номинальных емкостей (или суммарную емкость нескольких конденсаторов из этого ряда) такими, чтобы получившаяся частота раздела попадала в указанные выше частотные интервалы.
| Тип конденсатора | Емкость, мкФ |
| МБМ | 0,6 |
| МБГО, МВГП | 1; 2; 4; 10 |
| МБГП | 15; 26 |
| МБГО | 20; 30 |
Емкости конденсаторов фильтров С1. С4 для различных сопротивлений головок и соответствующие значения частот раздела приведены в табл 2.
С4 для различных сопротивлений головок и соответствующие значения частот раздела приведены в табл 2.
| Zг,0м | 4.0 | 4.5 | 5.0 | 6.5 | 8.0 | 12,5 | 15 |
| С1,C2, мкф | 40 | 30 | 30 | 20 | 20 | 15 | |
| fp1, Гц | 700 | 840 | 790 | 580 | 700 | – | 520 |
| С3,С4, мкф | 5 | 5 | 4 | 4 | 3 | 2 | 1,5 |
| fр2,кГц | 5,8 | 5,2 | 5 | 4,4 | 4,8 | 4,6 | 5,4 |
Легко видеть, что все значения емкостей могут быть либо непосредственно взяты из номинального ряда емкостей. либо получены параллельным соединением не более чем двух конденсаторов (см. табл. 1).
После того как емкости конденсаторов выбраны, определяют индуктивности катушек в миллигенри по формулам:
Поскольку полное сопротивление головки является частотнозависимой величиной, для расчета обычно принимают указанное в паспорте головки номинальное сопротивление Zг, оно соответствует минимальному значению полного сопротивления головки в диапазоне частот выше частоты основного резонанса до верхней граничной частоты рабочей полосы.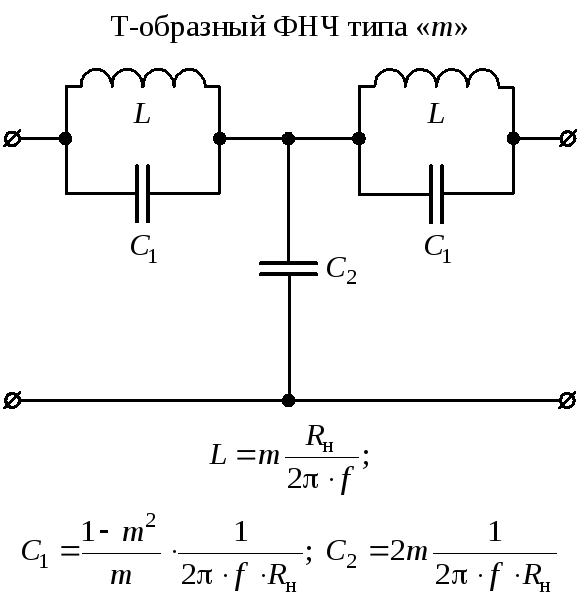 При этом надо иметь в виду, что фактическое номинальное сопротивление различных образцов головок одного и того же типа может отличаться от паспортного значения на ±20%.
При этом надо иметь в виду, что фактическое номинальное сопротивление различных образцов головок одного и того же типа может отличаться от паспортного значения на ±20%.
В некоторых случаях радиолюбителям приходится использовать в качестве высокочастотных головок имеющиеся динамические головки с номинальным сопротивлением, отличающимся от номинальных сопротивлений низкочастотной и высокочастотной головок. При этом согласование сопротивлений осуществляют, подключая высокочастотную головку В3 и конденсатор С4 к различным выводам катушки L4 (рис. 2), т. е. эта катушка фильтра играет одновременно роль согласующего автотрансформатора. Катушки можно намотать на круглых деревянных, пластмассовых или картонных каркасах с щечками из гетинакса. Нижнюю щечку следует сделать квадратной; так ее удобно крепить к основанию – гетинаксовой плате, на которой крепят конденсаторы и катушки. Плату крепят шурупами ко дну ящика громкоговорителя. Во избежание дополнительных нелинейных искажений катушки должны выполняться без сердечников из магнитных материалов.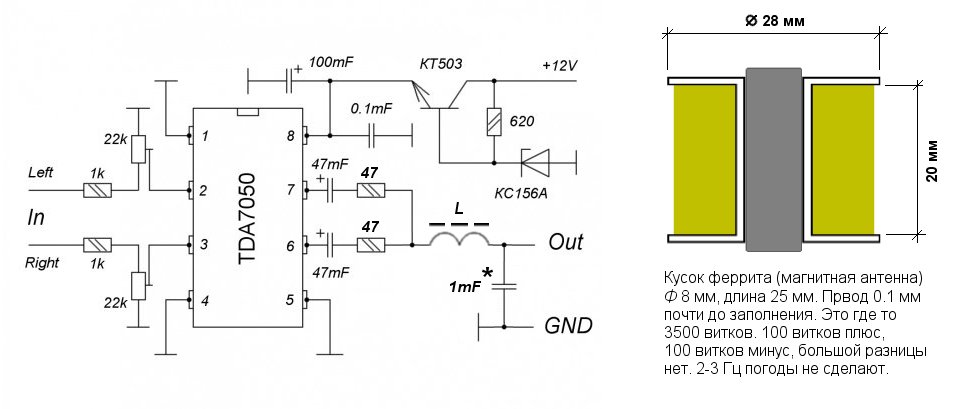
Пример расчета фильтра.
В качестве низкочастотной головки громкоговорителя используется динамическая головка 6ГД-2, номинальное сопротивление которой Zг=8 Ом. в качестве среднечастотной – 4ГД-4 с таким же значением Zг и в качестве высокочастотной – ЗГД-15, для которой Zг=6,5 Ом. Согласно табл. 2 при Zг=8 Ом и емкости С1=С2=20 мкф fp1=700 Гц, а при емкости С3=С4=3 мкф fр2=4,8 кГц. В фильтре можно применить конденсаторы МБГО со стандартными емкостями (С3 и С4 составляют из двух конденсаторов).
По приведенным выше формулам находим: L1=L3=2,56 мГ; L2=L4=0,375 мГ (для автотрансформатора L4 – это значение индуктивности между выводами 1-3).
Коэффициент трансформации автотрансформатора
На рис. 3 показана зависимость уровня напряжения на звуковых катушках головок от частоты для трехполосной системы, соответствующей примеру расчета. Амплитудно-частотные характеристики низкочастотной, среднечастотной и высокочастотной областей фильтра обозначены соответственно НЧ, СЧ и ВЧ.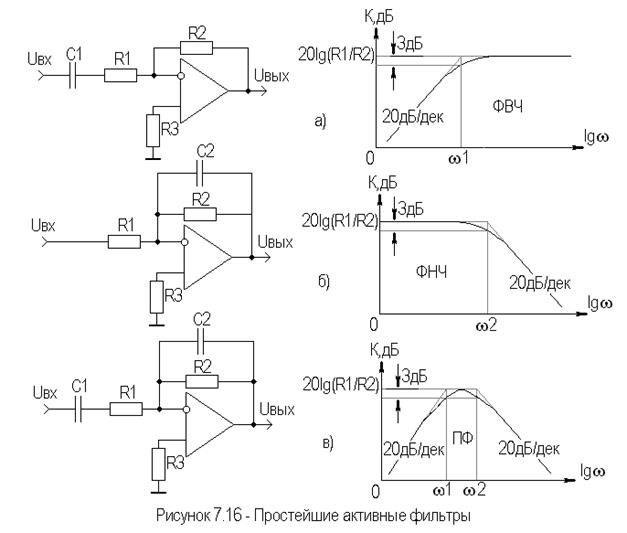 На частотах раздела затухание фильтра равно 3,5 дБ (при рекомендуемом затухании 3 дБ).
На частотах раздела затухание фильтра равно 3,5 дБ (при рекомендуемом затухании 3 дБ).
Отклонение объясняется отличием полных сопротивлений головок и емкостей конденсаторов от заданных (номинальных) значений и индуктивностей катушек от полученных расчетом. Крутизна спада кривых НЧ и СЧ составляет 9 дБ на октаву и кривой ВЧ – 11 дБ на октаву. Кривая ВЧ соответствует несогласованному включению громкоговорителя 1 ГД-3 (в точки 1-3). Как видно, в этом случае фильтр вносит дополнительные частотные искажения.
Примечание от авторов:
В приводимой методике расчета принято, что среднее звуковое давление при одной и той же подводимой электрической мощности для всех головок имеет примерно одинаковое значение. Вели же звуковое давление, создаваемое какой-либо головкой, заметно больше, то для выравнивания частотной характеристики громкоговорителя по звуковому давлению эту головку рекомендуется подключать к фильтру через делитель напряжения, входное сопротивление которого должно быть равно принятому при расчете номинальному сопротивлению головок.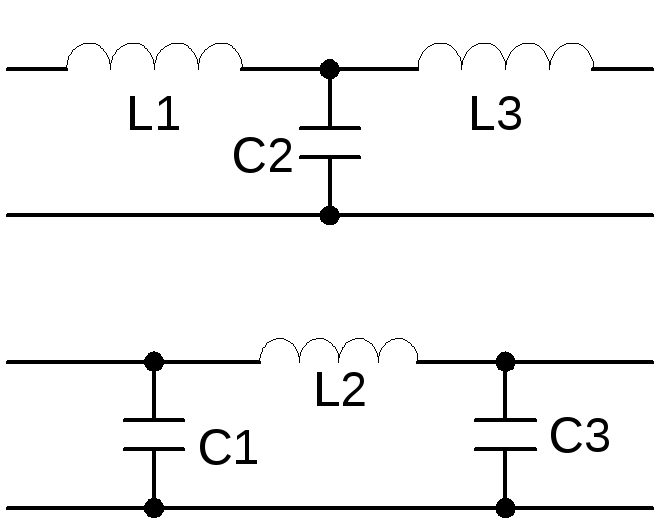
РАДИО N 9, 1977 г., с.37-38 E. ФРОЛОВ, г. Москва
Расчет кроссовера для акустики75
Расчет кроссовера для акустики, как известно, очень важная операция. На свете не существует идеальных акустических систем, способных воспроизводить частотный диапазон полностью.
И тогда на помощь приходят отдельные участки спектра динамиков. К примеру, если надо воспроизводить НЧ, применяют сабвуфер, а чтобы воспроизвести ВЧ, устанавливают мидбасы.
Когда все эти динамики вместе взятые начинают играть, то может произойти путаница перед поступлением на тот или иной излучатель. По этой причине и необходим бывает активный или пассивный кроссовер для акустики.
В этой статье мы узнаем, для чего нужен расчет фильтра, рассмотрим пассивные кроссоверы, узнаем как они строятся на катушках индуктивности и конденсаторах.
Расчет кроссовера
Кроссоверы для акустики авто самодельные
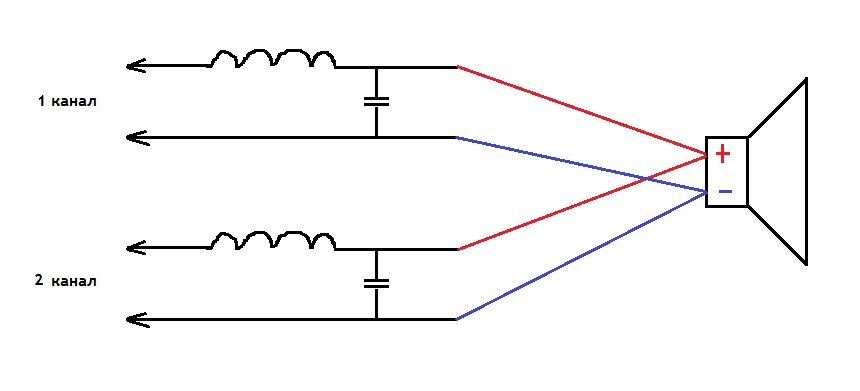
Чтобы подключить 2-полосную(см.Акустическая двухполосная система и ее преимущества) или другую акустику с большим количеством полос к 1 каналу усилителя или ГУ, нужно некое отдельное устройство, разделяющее сигнал.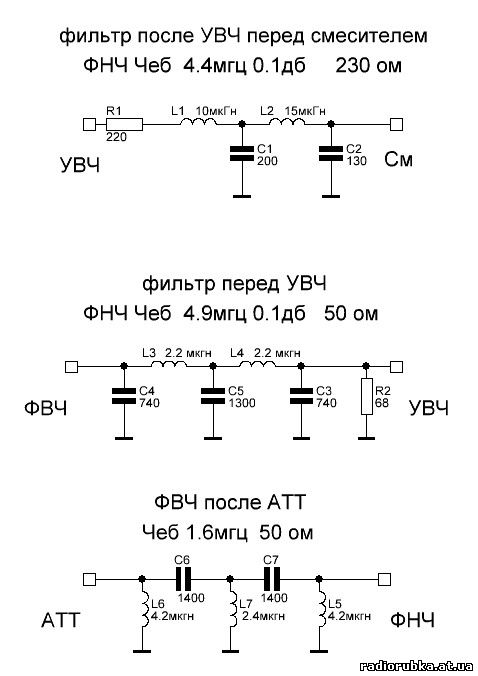 При этом оно должно выделять для каждой полосы свои частоты. Именно такие устройства и называются фильтрами или кроссоверами.
При этом оно должно выделять для каждой полосы свои частоты. Именно такие устройства и называются фильтрами или кроссоверами.
Примечание. В комплекте с компонентной акустикой, как правило, уже идет пассивный кроссовер. Его готовил производитель и он рассчитан уже изначально.
Но что делать, если нужно разделить частоты по иной схеме (к примеру, если комплект акустики собран из отдельных компонентов)?
В этом случае речь идет о расчете кроссовера.Отметим сразу, что рассчитать кроссовер совершенно не сложно и даже можно самостоятельно изготовить его.
Кроссоверы для акустики на авто Пионер профессиональные
Ниже приводится инструкция о том, как рассчитать кроссовер:
- Скачиваем специальную программу. Это может быть Crossover Elements Calculator на компьютер;
Специальная программа для расчета кроссовера Crossover Elements Calculator
- Вводим сопротивления низкочастотного и высокочастотного динамиков.
 Сопротивление – это номинальное значение сопротивления акустики, выражаемое в Ом. Как правило, средним значением является 4 Ом;
Сопротивление – это номинальное значение сопротивления акустики, выражаемое в Ом. Как правило, средним значением является 4 Ом; - Вводим частоту раздела кроссовера. Здесь полезно будет знать, что частоту надо вводить в Гц, но ни в коем случае не в кГц.
Примечание. Если кроссовер второго порядка, то надо еще ввести тип кроссовера.
- Получить ожидаемый результат можно, нажав на кнопку расчета.
Кроме того, надо знать следующее:
- Емкость конденсаторов, а вернее их значение вводится в Фарадах;
- Индуктивность рассчитывается в Генри (mH).
Схема расчета фильтра выглядит примерно так:
Как рассчитать фильтр
Фильтры разного порядка
Чтобы ясно понимать схему расчета кроссовера(см.Самодельные кроссоверы для акустики и их предназначение), нужно понимать разницу между фильтрами разного порядка. Об этом и пойдет речь ниже.
Примечание.
Существуют несколько порядков кроссовера. В данном случае порядок означает параметр кроссовера, который характеризует его способность ослаблять не нужные частотные сигналы.
Первый порядок
Схема 2-х полосного кроссовера этого порядка выглядит следующим образом:
2-полосный кроссовер 1-го порядка
По схеме видно, что ФНЧ или фильтр низких частот построен на катушке индуктивности, а фильтр высоких частот – на конденсаторе.
Примечание. Такой выбор компонентов не случаен, так как сопротивление катушки индуктивности повышается прямо пропорционально увеличению частоты. А вот что касается конденсатора, то здесь обратно пропорционально. Получается, что такая катушка отлично пропускает НЧ, а конденсатор отвечает за пропуск ВЧ. Все просто и оригинально.
Фильтр частот по схеме 1-го порядка
Следует также знать, что кроссоверы первого порядка, а вернее их номинал, зависит от выбранной частоты разделения и величины сопротивления колонки.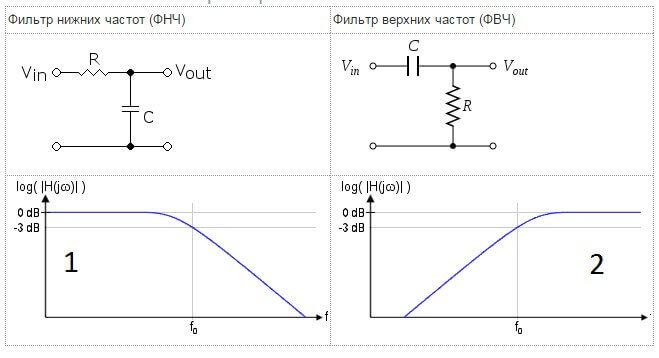 Проектируя ФНЧ, надо в первую очередь обратить внимание на частоту среза НЧ и СЧ динамиков(см.Как выбрать динамики для автомагнитолы своими силами).
Проектируя ФНЧ, надо в первую очередь обратить внимание на частоту среза НЧ и СЧ динамиков(см.Как выбрать динамики для автомагнитолы своими силами).
А вот проектируя ФВЧ, надо аналогичным образом поступить уже с ВЧ.
Пассивный кроссовер
Что такое в акустике кроссовер
Наиболее доступной на сегодня считается именно пассивная фильтрация, так как она сравнительно проста в реализации. С другой стороны, не все так просто.
Речь идет о следующих недостатках:
- Согласовать параметры и значение фильтров с характеристиками излучателей колонок очень сложная штука;
- В процессе эксплуатации может наблюдаться нестабильность параметров акустической системы. К примеру, если повысится сопротивление звуковой катушки при нагреве. В связи с этим значительно ухудшится достигнутое в процессе разработки согласование;
- Фильтр, обладая внутренним сопротивлением, забирает некоторую часть выходной мощности усилителя. Одновременно с этим ухудшается демпфирование, а это сказывается на качестве звучания и четкости передачи нижнего регистра.

Что такое кроссовер в акустике
Как известно, на сегодняшний день самыми распространенными акустическими системами считаются 2-х компонентные варианты.
В них фильтр разделяет звуковой сигнал на два диапазона:
- Первый диапазон предназначается исключительно для низких и средних частот. В данном случае используется кроссовер для нижних частот или ФНЧ;
- Второй диапазон предназначен для ВЧ. Здесь уже используется другой фильтр ФВЧ.
Примечание. Вариантов реализации фильтра может быть несколько, но он все должно отвечать определенным канонам.
Ниже приводится список требований, которым обязательно должен соответствовать кроссовер:
- Фильтр не должен оказывать влияния на частотный спектр и волну выходящего аудиосигнала;
- Должен создавать для усилителя, независимую от частоты нагрузку активного характера;
- Должен суметь обеспечивать вместе с акустическими системами формирование диаграммы направленности.
 Это должно быть реализовано так, чтобы до слушателя доходило максимум излучения.
Это должно быть реализовано так, чтобы до слушателя доходило максимум излучения.
Кроссовер АС очень важен
Из статьи мы узнали, как проводится расчет кроссовера акустических систем своими руками. В процессе работ будет полезно также изучить схемы, посмотреть видео обзор и фото – материалы.
Если научиться самостоятельно рассчитывать фильтр, платить за услуги специалистам не придется. Таким образом, цена операции сводится к минимуму, ведь надо только приложить немного терпения и уделить некоторое время изучению.
Фильтр низких частот | Микросхема
Как можете видеть, уважаемые радиолюбители, в комментариях к схемам усилителей звуковой частоты очень часто проскакивают вопросы новичков такого характера: «посоветуйте, как сделать фильтр низких частот для этого усилителя?»
На такие вопросы приходится отвечать, обычно, типовыми фразами или отсылкой к имеющимся схемам, за что, конечно же, прошу прощения. У нас на сайте есть достаточное количество схем, чтобы можно было без труда собрать качественный ФНЧ для использования с любым усилителем мощности. Приведу ссылки на простые и, в то же время, довольно кондиционные фильтры низких частот:
Приведу ссылки на простые и, в то же время, довольно кондиционные фильтры низких частот:
Неплохие результаты показывают наипростейшие фильтры низких частот: схемы в комментариях к статье.
Однако сегодня мы с вами будем собирать достаточно эффективный фильтр низких частот для сабвуфера.
Всем известно, что акустический спектр расположен в диапазоне 20…20 000 Гц. 20 Гц – это достаточно низкая частота. Вообще, на низких частотах ухудшается восприятие направленности звука или, скажем так, его локализация. Здесь я немного поясню. На частотах ниже 150 Гц разделение звукового сигнала по каналам не имеет смысла. Акустические системы, оснащённые сабвуфером, имеют, как правило, конфигурации 2.1, 5.1, 7.1. Сабвуфер в них один. В сабвуферном канале идёт смешение всех других каналов и срез частот от 20 Гц (не всегда) до какой-то верхней частоты (100, 130, 150 Гц).
Для качественного воспроизведения звукового тракта выделение низких частот в отдельный канал обязательно. В качестве удачного решения я предлагаю такую схему ФНЧ, ограничивающего частоту акустического спектра в районе 20 — 100 Гц.
На схеме можно видеть два каскада, каждый из которых собран на операционном усилителе. В качестве активного элемента в схеме применяется сдвоенный операционный усилитель типа TL082, TL062, NE5532.
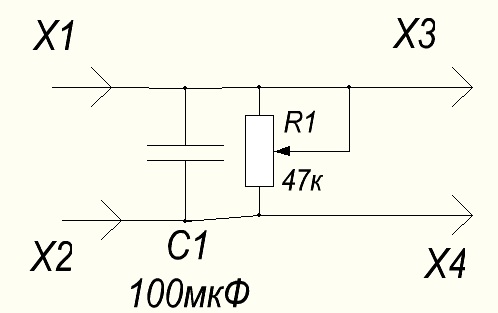
Первый ОУ служит для смешения каналов и усиления входного сигнала (предусиления). Уровень выходного сигнала, снимаемого с первого операционника, зависит от сопротивления переменного резистора R3 номиналом 47 кОм.
На втором ОУ собран непосредственно сам фильтр среза. Частота среза зависит от номиналов деталей обвязки данного операционного усилителя. Частоту можно регулировать в достаточно широких пределах: от 30 Гц до 150 Гц. Регулировать частоту среза можно сдвоенным переменным резистором R5, R7 номиналом 22 кОм.
Перечень радиодеталей, используемых в фильтре низких частот:
- R1 = 39 кОм
- R2 = 39 кОм
- R3 = 47 кОм
- R4 = 10 Ом
- R5 = 22 кОм
- R6 = 4,7 кОм
- R7 = 22 кОм
- R8 = 4,7 кОм
- R9 = 10 Ом
- R10 = 220 Ом
- C1 = 39 пФ
- C2 = 0.
 1 мкФ
1 мкФ - C3 = 0.1 мкФ
- C4 = 0.2 мкФ
- C5 = 0.4 мкФ
- C6 = 0.1 мкФ
- C7 = 0.1 мкФ
- IC1 = TL062
Схема очень чувствительна к качеству радиодеталей, особенно к конденсаторам. Их допуск должен быть не более 5%. Проверить работоспособность фильтра можно с помощью звукового генератора. В итоге получается универсальный ФНЧ для сабвуферного канала практически для любой акустической системы.
Топология печатной платы и расположение радиодеталей на ней:
Обсуждайте в социальных сетях и микроблогах
Метки: акустика, предусилитель, сабвуфер, фильтр НЧ
Радиолюбителей интересуют электрические схемы:
Активные фильтры к сабвуферам
Кроссовер для сабвуфера
Простейшие электрические фильтры — Студопедия
Электрические фильтры — это устройства, которые пропускают на выход сигналы одних частот и не пропускают сигналы других частот.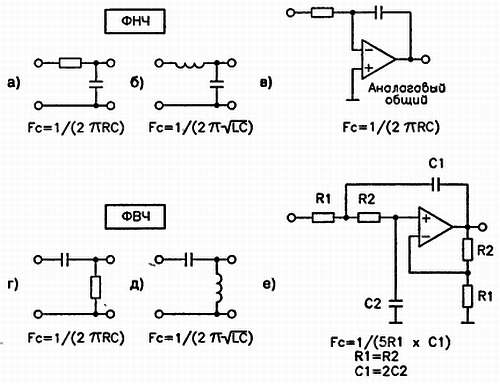 По виду АЧХ фильтры разделяются на фильтры нижних частот (НЧ), верхних частот (ВЧ), полосовые фильтры (ПЧ) и др.
По виду АЧХ фильтры разделяются на фильтры нижних частот (НЧ), верхних частот (ВЧ), полосовые фильтры (ПЧ) и др.
Фильтры нижних частот (НЧ).
Фильтр нижних частот без изменения передает сигнал нижних частот, включая и нулевую частоту (постоянный сигнал), а на высоких частотах обеспечивает затухание сигналов. На рис.2.3, а изображена схема простого фильтра НЧ. Сопротивление емкости С зависит от частоты входного сигнала и равно хС = 1 / ωC . Емкость С вместе с резистором R образуют делитель напряжения. Для частоты ω = 0 сопротивление емкости равно бесконечности. И весь сигнал с входа схемы поступает на выход. С увеличением частоты сопротивление емкости уменьшается, и все большая его часть будет замыкаться на землю. И в пределе, когда ω = ∞, сопротивление емкости будет равно 0, напряжение на выходе также будет равно 0. Таким образом, схема обладает свойствами фильтра НЧ.
Для расчета частотной характеристики схемы воспользуемся методом комплексных амплитуд.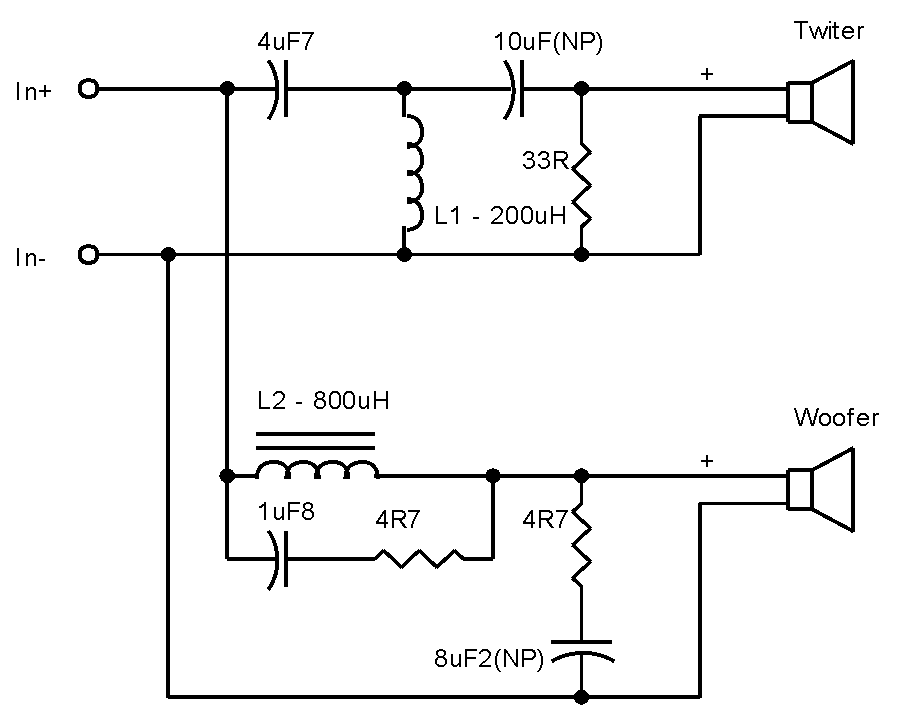 По схеме рис.2.3,б, используя формулу для делителя напряжения, найдем выходной сигнал
По схеме рис.2.3,б, используя формулу для делителя напряжения, найдем выходной сигнал
.
Отсюда найдем комплексный коэффициент передачи
,
где Т = RC – постоянная времени RC – цепочки.
АЧХ представляет собой модуль комплексного коэффициента передачи ,
а ФЧХ аргумент комплексного коэффициента передачи .
На рис.2.4 показаны частотные характеристики ФНЧ для R = 1 кОм, и С = 1 мкФ.
На АЧХ фильтра можно выделить три области частот: полосу пропускания, переходную область, и полосу подавления сигнала. В полосе пропускания допускается снижение коэффициента передачи в раза. На АЧХ рис.2.4 такое уменьшение коэффициента передачи происходит на частое 158,489 ≈ 159 Гц. Частота, на которой коэффициент передачи уменьшается в раз, называется частотой среза. Частота среза разделяет область пропускания фильтра от переходной области. Полоса пропускания фильтра НЧ лежит от 0 Гц до частоты среза fc.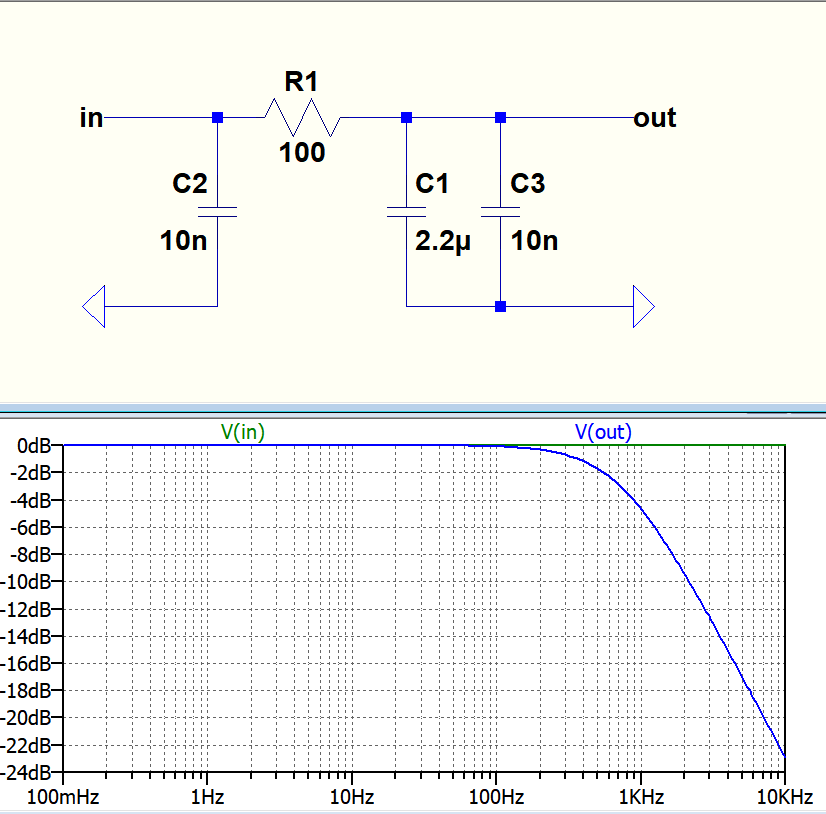 Частота среза RC –фильтра НЧ равна fc. = 1/ 2πRC или круговая частота среза ωс = 1/RC = 1 / T. В этом легко убедиться, если в формулу АЧХ фильтра вместо ω подставить ωс = 1/RC, то получим . Это означает, что на частоте ωс = 1/RC, коэффициент передачи уменьшился в раз.
Частота среза RC –фильтра НЧ равна fc. = 1/ 2πRC или круговая частота среза ωс = 1/RC = 1 / T. В этом легко убедиться, если в формулу АЧХ фильтра вместо ω подставить ωс = 1/RC, то получим . Это означает, что на частоте ωс = 1/RC, коэффициент передачи уменьшился в раз.
Частота, которая разделяет переходную область фильтра от полосы подавления сигнала, не нормируется. Она определяется в зависимости от требований, предъявляемых к АЧХ фильтра в конкретном применении. Для сравнения различных фильтров эта частота иногда определяется на уровне 0,01 от коэффициента передачи на нулевой частоте.
Обычно АЧХ необходимо анализировать в широком диапазоне частот. Например, для операционного усилителя широкого применения, от единиц Гц до десятков МГц. В этом случае удобно ось частот представлять в логарифмическом масштабе lg f или lgω, как показано на графике рис.2. 4. Коэффициент передачи при этом измеряется в обычном линейном масштабе. Однако, если коэффициент передачи (усиления) изменяется в очень широких пределах, как например, в операционном усилителе, то его удобно выражать в логарифмическом масштабе:
Однако, если коэффициент передачи (усиления) изменяется в очень широких пределах, как например, в операционном усилителе, то его удобно выражать в логарифмическом масштабе:
L(ω) = 20lg A.
Единицы измерения – децибелы (дБ), десятая часть бела. Зависимость коэффициента усиления от частоты входного сигнала в логарифмическом масштабе называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ).
Что собой представляет единица измерения бел, и почему коэффициент перед логарифмом равен 20, а не 10 как следовало бы ожидать. Единица измерения 1 Бел соответствует отношению мощностей в 10 раз:
1 Б = P2 / P1 = 10.
Так как 1 Б – это очень большая величина, то на практике используют более мелкие величины децибелы (в одном беле содержится 10 дБ). Поэтому в коэффициенте усиления по мощности коэффициент пропорциональности равен 10:
Lp = 10 lg P2 / P1.
Но у нас коэффициент усиления, это отношение амплитуд токов или напряжений. А для токов и напряжений мощность пропорциональна квадрату токов или напряжений
А для токов и напряжений мощность пропорциональна квадрату токов или напряжений
P = UI = U2/R = I2R.
При отношении амплитуд в 10 раз мощность увеличивается в 100 раз, т.е. на 2 Бела или на 20 децибел:
U2/U1 = 10, P2/P1 = (U2/U1)2 = (10)2 = 100.
Поэтому в формуле для логарифмического коэффициента усиления появился множитель 20, а не 10.
Логарифмические единицы удобны еще тем, что если известны коэффициенты усиления отдельных каскадов или узлов усилителя и общий коэффициент усиления равен произведению этих коэффициентов, то в логарифмическом масштабе коэффициент усиления находят как алгебраическую сумму логарифмических коэффициентов усиления отдельных каскадов.
На рис.2.5 представлена ЛАЧХ RC фильтра НЧ.
Частота среза фильтра определяется на уровне -3 дБ от максимального значения коэффициента усиления в полосе пропускания. Это видно из показаний слайдера правого курсора. Величина – 3 дБ в логарифмическом масштабе соответствует коэффициенту усиления в линейном масштабе, то есть L = 20lg 0,707 = -3 дБ. Из ЛАЧХ хорошо видно как подавляется сигнал на высоких частотах. Так на частоте 10 кГц логарифмический коэффициент усиления почти равен – 40 дБ, что соответствует значению 0,01 в линейном масштабе. Попробуйте определить коэффициент усиления на этой частоте по АЧХ на рис.2.4.
Величина – 3 дБ в логарифмическом масштабе соответствует коэффициенту усиления в линейном масштабе, то есть L = 20lg 0,707 = -3 дБ. Из ЛАЧХ хорошо видно как подавляется сигнал на высоких частотах. Так на частоте 10 кГц логарифмический коэффициент усиления почти равен – 40 дБ, что соответствует значению 0,01 в линейном масштабе. Попробуйте определить коэффициент усиления на этой частоте по АЧХ на рис.2.4.
Фазочастотные характеристики в обоих случаях строятся в линейном масштабе. Из фазочастотных характеристик видно, что наибольшее изменение фазы происходит на частоте среза фильтра.
Фильтры верхних частот (ВЧ). Фильтр верхних частот без изменения передает сигнал верхних частот, а на низких частотах обеспечивает затухание сигналов. Схема простого RC фильтра верхних частот представлена на рис.2.6. Аналогично, как и для фильтра нижних частот найдем выходной сигнал
.
Отсюда найдем комплексный коэффициент передачи
,
где Т = RC – постоянная времени RC – цепочки.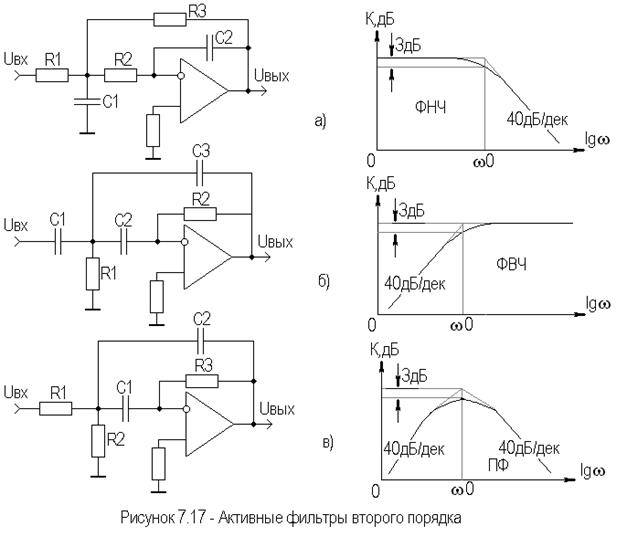
АЧХ представляет собой модуль комплексного коэффициента передачи ,
а ФЧХ аргумент комплексного коэффициента передачи .
На рис.2.7. Показаны частотные характеристики фильтра ВЧ ( R = 1 кОм, и С = 1 мкФ) в логарифмическом масштабе.
Частота среза фильтра определяется, так же как и для фильтра НЧ и равна с = 1/RC = 1 / T или fact. = 1/ 2πRC = 1/(6,28 ?1 кОм ?1 мкФ) = 159 Гц. На графике АЧХ частота среза определяется на уровне – 3 дБ от максимального значения коэффициента усиления. Положение левого курсора определяет частоту среза, так как разность между показаниями коэффициента усиления правого и левого курсора равна 3,019 ≈ 3 дБ.
Полосовой фильтр. Соединяя последовательно фильтр верхних и низких частот с перекрывающимися амплитудно-частотными характеристиками можно получить полосовой фильтр. Полосовой фильтр пропускает сигнал в некоторой полосе частот и подавляет сигнал на низких и высоких частотах. На рис 8. показана схема полосового фильтра.
Найдем комплексный коэффициент усиления схемы.
.
Введем обозначение ωRC = Ω. Раскрывая скобки, получим
Комплексный коэффициент усиления равен
.
АЧХ представляет собой модуль комплексного коэффициента передачи ,
ФЧХ определяется из выражения .
Коэффициент максимальный при Ω = 1. Следовательно, резонансная частота f0 = 1/ 2πRC. Коэффициент усиления на резонансной частоте равен A(f0) = 1/3, а фазовый сдвиг равен 0.
На рис.9 приведены частотные характеристики полосового фильтра при R=1 кОм и С = 1 мкФ.
Резонансная частота фильтра равна 159,591 Гц. АЧХ полосового фильтра имеет две частоты среза, которые располагаются слева и справа от резонансной частоты f0, и также определяются на уровне – 3 дБ относительно максимального значения коэффициента усиления.
Электрические фильтры (Лекция №15)
Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания и нагрузкой и служащий для беспрепятственного (с малым затуханием) пропускания токов одних частот и задержки (или пропускания с большим затуханием) токов других частот.
Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием), называется полосой пропускания или полосой прозрачности; диапазон частот, пропускаемых с большим затуханием, называется полосой затухания или полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.
В качестве пассивных фильтров обычно применяются четырехполюсники на основе катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров, используемых при больших сопротивлениях нагрузки.
Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.
Для упрощения анализа будем считать, что фильтры составлены из идеальных катушек индуктивности и конденсаторов, т.е. элементов соответственно с нулевыми активными сопротивлением и проводимостью. Это допущение достаточно корректно при высоких частотах, когда индуктивные сопротивления катушек много больше их активных сопротивлений ( ), а емкостные проводимости конденсаторов много больше их активных проводимостей ( ).
Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной Т- или П-образной схеме, т.е. при или (см. лекцию №14). В этой связи при изучении фильтров будем использовать введенные в предыдущей лекции понятия коэффициентов затухания и фазы.
Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.
Таблица 1. Классификация фильтров
|
Название фильтра |
Диапазон пропускаемых частот |
|
Низкочастотный фильтр (фильтр нижних частот) |
|
|
Высокочастотный фильтр (фильтр верхних частот) |
|
|
Полосовой фильтр (полосно-пропускающий фильтр) |
|
|
Режекторный фильтр (полосно-задерживающий фильтр) |
и , где |
В соответствии с материалом, изложенным в предыдущей лекции, если фильтр имеет нагрузку, сопротивление которой при всех частотах равно характеристическому, то напряжения и соответственно токи на его входе и выходе связаны соотношением
| . . | (1) |
В идеальном случае в полосе пропускания (прозрачности) , т.е. в соответствии с (1) , и . Следовательно, справедливо и равенство , которое указывает на отсутствие потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания (в полосе затухания) в идеальном случае , т.е. и .
Рассмотрим схему простейшего низкочастотного фильтра, представленную на рис. 1,а.
Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)
или конкретно для фильтра на рис. 1,а
| ; | (2) |
| ; | (3) |
| . | (4) |
Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что
.
Однако в соответствии с (2) — вещественная переменная, а следовательно,
| . | (5) |
Поскольку в полосе пропускания частот коэффициент затухания , то на основании (5)
.
Так как пределы изменения : , — то границы полосы пропускания определяются неравенством
,
которому удовлетворяют частоты, лежащие в диапазоне
| . | (6) |
Для характеристического сопротивления фильтра на основании (3) и (4) имеем
| . | (7) |
Анализ соотношения (7) показывает, что с ростом частоты w в пределах, определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается до нуля, оставаясь активным. Поскольку, при нагрузке фильтра сопротивлением, равным характеристическому, его входное сопротивление также будет равно , то, вследствие вещественности , можно сделать заключение, что фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших , как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.
На рис. 2 приведены качественные зависимости и .
Следует отметить, что вне полосы пропускания . Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство
| . | (8) |
Так как вне полосы прозрачности , то соотношение (8) может выполняться только при .
В полосе задерживания коэффициент затухания определяется из уравнения (5) при . Существенным при этом является факт постепенного нарастания , т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания будет отличен от нуля.
Другим вариантом простейшего низкочастотного фильтра может служить четырехполюсник по схеме на рис. 1,б.
Схема простейшего высокочастотного фильтра приведена на рис. 3,а.
Для данного фильтра коэффициенты четырехполюсника определяются выражениями
| ; | (9) |
| ; | (10) |
| . | (11) |
Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)
.
Данному неравенству удовлетворяет диапазон изменения частот
| . | (12) |
Характеристическое сопротивление фильтра
| , | (13) |
изменяясь в пределах от нуля до с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с в ограниченном диапазоне частот.
Вне области пропускания частот определяется из уравнения
| (14) |
при . Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.
Качественный вид зависимостей и для низкочастотного фильтра представлен на рис. 4.
Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.
Полосовой фильтр формально получается путем последовательного соединения низкочастотного фильтра с полосой пропускания и высокочастотного с полосой пропускания , причем . Схема простейшего полосового фильтра
приведена на рис. 5,а, а на рис. 5,б представлены качественные зависимости для него.
У режекторного фильтра полоса прозрачности разделена на две части полосой затухания. Схема простейшего режекторного фильтра и качественные зависимости для него приведены на рис.6.
В заключение необходимо отметить, что для улучшения характеристик фильтров всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой каскадно включенные четырехполюсники. При обеспечении согласованного режима работы всех n звеньев схемы коэффициент затухания такого фильтра возрастает в соответствии с выражением , что приближает фильтр к идеальному.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Каплянский А. Е. и др. Электрические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. -М.: Высш. шк., 1972. -448с.
Контрольные вопросы и задачи
- Для чего служат фильтры?
- Что такое полосы прозрачности и затухания?
- Как классифицируются фильтры в зависимости от диапазона пропускаемых частот?
- В каком режиме работают фильтры в полосе пропускания частот?
- Почему рассмотренные фильтры нельзя считать идеальными?
- Как можно улучшить характеристики фильтра?
- Определить границы полосы прозрачности фильтров на рис. 1,а и 3,а, если L=10 мГн, а С=10 мкФ.
Ответ: , .
Как создать простой фильтр нижних частот
Резюме: В этой статье показано, как создать простой фильтр нижних частот, начиная с частоты среза \ (f_c \) и полосы перехода \ (b \). Эта статья дополняется инструментом Filter Design , который позволяет вам создавать свои собственные пользовательские версии примера фильтра, показанного ниже, и загружать полученные коэффициенты фильтра.
Как создать простой фильтр нижних частот? Фильтр нижних частот предназначен для пропускания низких частот, но для остановки высоких частот.Теоретически, фильтр нижних частот perfect (т.е. perfect ) является фильтром sinc . Функция sinc ( нормализованное , следовательно, \ (\ pi \), как обычно при обработке сигналов) определяется как
.\ [\ mathrm {sinc} (x) = \ frac {\ sin (\ pi x)} {\ pi x}. \]
Фильтр sinc — это его масштабированная версия, которую я определю ниже. При свертке с входным сигналом синк-фильтр дает выходной сигнал, в который включены все частоты до частоты среза, а все более высокие частоты блокируются.Это связано с тем, что функция sinc является обратным преобразованием Фурье прямоугольной функции . Умножение частотного представления сигнала на прямоугольную функцию можно использовать для генерации идеальной частотной характеристики , поскольку при этом полностью удаляются частоты выше точки отсечки. И, поскольку умножение в частотной области эквивалентно свертке во временной области, фильтр sinc имеет точно такой же эффект.
Фильтр windowed-sinc , описанный в этой статье, является примером фильтра Finite Impulse Response ( FIR ).
Фильтр Sinc
Функция sinc должна быть масштабирована и дискретизирована, чтобы создать последовательность и превратить ее в (цифровой) фильтр. Импульсная характеристика sinc-фильтра определяется как
.\ [h [n] = 2f_c \ mathrm {sinc} (2f_cn), \]
где \ (f_c \) — частота среза. Частота среза должна быть указана как часть частоты дискретизации. Например, если частота дискретизации составляет 10 кГц, то \ (f_c = 0,1 \) приведет к удалению частот выше 1 кГц. Центральная часть sinc-фильтра с \ (f_c = 0.1 \) показан на рисунке 1.
Рисунок 1. Синк-фильтр.Проблема с фильтром sinc заключается в том, что он имеет бесконечную длину в том смысле, что его значения не опускаются до нуля. Это означает, что задержка фильтра также будет бесконечной, что сделает этот фильтр нереализуемым . Простое решение состоит в том, чтобы просто прекратить вычисление в определенный момент (эффективно , усекая фильтр), но это создает чрезмерную пульсацию . Лучшее решение — window sinc filter, что дает, как вы уже догадались, windowed-sinc filter .
Окно
Оконная функция — это функция, которая равна нулю за пределами некоторого интервала. Существует множество этих функций, настроенных для разных свойств, но я просто воспользуюсь хорошо известным окном Blackman , которое является хорошим выбором для общего использования. Он определяется как (для \ (N \) точек)
\ [w [n] = 0,42-0,5 \ cos \ left ({\ frac {2 \ pi n} {N-1}} \ right) +0,08 \ cos \ left ({\ frac {4 \ pi n}) {N-1}} \ right), \]
с \ (n \ in [0, \, N-1] \). Это показано на рисунке 2 для \ (N = 51 \).
Рисунок 2. Окно Блэкмана.Оконный фильтр из цинка
Окончательный оконный фильтр sinc будет просто произведением двух предыдущих выражений, как показано ниже (с фильтром sinc, сдвинутым в диапазон \ ([0, \, N-1] \)).
\ [h [n] = \ mathrm {sinc} \ left (2f_c \ left (n- \ frac {N-1} {2} \ right) \ right) \ left (0,42-0,5 \ cos \ left ({ \ frac {2 \ pi n} {N-1}} \ right) +0,08 \ cos \ left ({\ frac {4 \ pi n} {N-1}} \ right) \ right), \]
с \ (h [n] = 0 \) для \ (n \ notin [0, \, N-1] \). Я исключил коэффициент \ (2f_c \) из фильтра sinc, так как гораздо легче сначала игнорировать константы и нормализовать весь фильтр в самом конце, просто убедившись, что сумма всех коэффициентов равна единице, давая единичный коэффициент усиления фильтра, с
\ [h_ \ mathrm {нормализованный} [n] = h [n] / \ sum_ {i = 0} ^ {N-1} h [i].\]
Это приводит к нормализованному оконному синк-фильтру, показанному на рисунке 3.
Рисунок 3. Нормализованный оконный фильтр sinc.Ширина полосы перехода
Последняя задача — включить желаемую полосу пропускания (или спада ) фильтра. Чтобы упростить задачу, вы можете использовать следующее приближение отношения между полосой перехода \ (b \) и длиной фильтра \ (N \),
\ [b \ приблизительно \ frac {4} {N}, \]
с дополнительным условием, что лучше всего сделать \ (N \) нечетным.На самом деле это не требуется, но симметричный КИХ-фильтр нечетной длины имеет задержку, которая представляет собой целое число отсчетов, что позволяет легко сравнить отфильтрованный сигнал с исходным. Установка \ (N = 51 \) выше была достигнута установкой \ (b = 0,08 \). Что касается \ (f_c \), параметр \ (b \) должен быть указан как часть частоты дискретизации. Следовательно, для частоты дискретизации 10 кГц установка \ (b = 0,08 \) приводит к ширине полосы перехода около 800 Гц, что означает, что фильтр переходит от пропускания частот к их блокированию в диапазоне около 800 Гц.Значения для \ (f_c \) и \ (b \) в этой статье были выбраны, чтобы сделать цифры как можно более ясными. Частотная характеристика последнего фильтра (с \ (f_c = 0,1 \) и \ (b = 0,08 \)) показана на рисунке 4.
Рисунок 4. Частотная характеристика в линейной (слева) и логарифмической (справа) шкале.Код Python
В Python все эти формулы можно реализовать кратко.
из отдела импорта __future__
импортировать numpy как np
fc = 0.1 # Частота среза как часть частоты дискретизации (в (0, 0.5)).
b = 0,08 # Полоса перехода, как часть частоты дискретизации (в (0, 0,5)).
N = int (np.ceil ((4 / b)))
если не N% 2: N + = 1 # Убедитесь, что N нечетно.
n = np.arange (N)
# Вычислить фильтр sinc.
h = np.sinc (2 * fc * (n - (N - 1) / 2))
# Вычислить окно Блэкмана.
w = 0,42 - 0,5 * np.cos (2 * np.pi * n / (N - 1)) + \
0,08 * np.cos (4 * np.pi * n / (N - 1))
# Умножить фильтр sinc на окно.
ч = ч * ш
# Нормализовать, чтобы получить единичное усиление.
h = h / np.sum (h) Применение фильтра \ (h \) к сигналу \ (s \) путем свертки обеих последовательностей может быть таким же простым, как запись одной строки:
В приведенном выше скрипте Python я вычисляю все полностью, чтобы показать вам, что именно происходит, но на практике доступны ярлыки.Например, окно Блэкмана может быть вычислено с w = np.blackman (N) .
В следующей статье «Как создать простой фильтр верхних частот» я преобразовал этот фильтр нижних частот в фильтр верхних частот, используя спектральную инверсию . Затем оба типа фильтров объединены в документе
Как создать простые полосовые фильтры и фильтры отклонения полосы.Инструмент для проектирования фильтров
Эта статья дополнена средством создания фильтров. Поэкспериментируйте с разными значениями для \ (f_c \) и \ (b \), визуализируйте полученные фильтры и загрузите коэффициенты фильтров.Попробуй это сейчас!
Конструктор фильтров.Объясните различные типы фильтров нижних частот
Фильтры нижних частот
Самый простой подход к созданию фильтра — использовать пассивные компоненты, такие как резисторы, конденсаторы и катушки индуктивности. В ВЧ диапазоне работает неплохо, однако на более низких частотах дроссели создают проблемы. Поскольку для более низких частот необходимо увеличить индуктивность, что требует большего количества витков провода. Он увеличивает последовательное сопротивление, которое ухудшает характеристики индуктора.
Катушки индуктивностиAF физически больше и тяжелее, а потому дороги.
Фильтры нижних частот бывают многих типов, таких как R-C, R-L, инвертированный L-тип, T-тип и π-тип.
Цепь фильтра нижних частот R-C
Простой фильтр нижних частот R-C или LPF может быть легко изготовлен путем последовательного соединения одного резистора с одним конденсатором, как показано ниже.
В этой схеме входной сигнал (Vin) подается на последовательную комбинацию резистора и конденсатора, а выходной сигнал (Vout) передается только через конденсатор.
Этот тип фильтра обычно известен как «фильтр первого порядка» или «однополюсный фильтр».
Почему первого порядка или однополюсного?
Потому что он имеет в цепи только «один» реактивный компонент, конденсатор.
Как мы уже знаем, реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, в то время как значение резистора остается постоянным при изменении частоты.
На низких частотах емкостное реактивное сопротивление (Xc) конденсатора будет очень большим по сравнению с сопротивлением резистора R.Это означает, что потенциал напряжения Vc на конденсаторе будет намного больше, чем падение напряжения Vr, возникающее на резисторе.
На высоких частотах верно обратное: Vc мало, а Vr велико из-за изменения значения емкостного реактивного сопротивления.
При нулевой частоте конденсатор действует как разомкнутая цепь, и выход такой же, как вход.
Однако с увеличением частоты емкостное реактивное сопротивление уменьшается, а значит, и выходное напряжение. На бесконечной частоте емкостное реактивное сопротивление цепи будет равно нулю, и, следовательно, выходное напряжение также будет нулевым.
Поскольку он пропускает низкочастотные сигналы и блокирует высокочастотные сигналы, он называется фильтром нижних частот.
Емкостное реактивное сопротивление конденсатора в Ом определяется как
.Для последовательной цепи, состоящей из одного резистора, соединенного последовательно с одним конденсатором, полное сопротивление Z схемы рассчитывается как:
Следовательно, выходное напряжение на конденсаторе определяется как:
По этой формуле мы можем рассчитать выходное напряжение на любой частоте.
Частотная характеристика фильтра низких частот
Выше мы уже обсуждали, что по мере увеличения частоты, подаваемой на RC-цепь, напряжение на конденсаторе падает, и, следовательно, выходное напряжение (Vout) из схемы уменьшается.
Построив график зависимости выходного напряжения от различных значений входной частоты, можно найти функцию Frequency Response Curve или Bode Plot схемы фильтра нижних частот, как показано ниже.
Как видно из приведенного выше рисунка, частотная характеристика фильтра почти плоская для низких частот, и весь входной сигнал передается непосредственно на выход, что приводит к усилению почти 1, называемому единицей, пока не достигнет его Частота среза точки (ƒc).
Это связано с тем, что реактивное сопротивление конденсатора высокое на низких частотах и блокирует любой ток, протекающий через конденсатор.
После этой точки отсечки частота отклика схемы уменьшается до нуля с наклоном спада -20 дБ / декада или (-6 дБ / октава).Обратите внимание, что угол наклона, этот спад -20 дБ / декада всегда будет одинаковым для любой комбинации RC.
Любые высокочастотные сигналы выше этой граничной частоты, подаваемые на схему фильтра нижних частот, будут сильно ослабляться, то есть они быстро уменьшаются. Это происходит потому, что на очень высоких частотах реактивное сопротивление конденсатора становится настолько низким, что возникает эффект короткого замыкания на выходных клеммах, что приводит к нулевому выходу.
Частота отсечки определяется как точка частоты, в которой емкостное реактивное сопротивление и сопротивление равны, т.е.е. R = Xc. На этой частоте среза фазовый угол составляет 45 o , а выходная мощность составляет половину входной мощности. Выходное напряжение составляет 0,707 максимального значения напряжения V max .
Эта частота среза fc задается как:
Цепь фильтра нижних частот, правый-левый
Схема низкочастотного R-L контура показана на рис. ниже.
В этой схеме выходное напряжение снимается через сопротивление R.
Поскольку реактивное сопротивление, обеспечиваемое катушкой индуктивности L, увеличивается с увеличением частоты, это позволяет частотам до частоты среза fc проходить через катушку без особого сопротивления, но обеспечивает высокое реактивное сопротивление к частотам выше частоты среза.
Выходной сигнал, развиваемый на резисторе R, определяется следующим уравнением:
Частота отсечки fc определяется как:
Частота среза возникает, когда выходное напряжение V max = 0,707 входного напряжения, R = X L , V R = V L и фазовый угол импеданса составляет 45 o .
Перевернутый контур фильтра L-типа
В этой схеме фильтра используются дроссель и конденсатор.Схема перевернутой цепи фильтра L-типа показана на рис. ниже.
Поскольку дроссель обеспечивает высокое реактивное сопротивление высоких частот, он блокирует их, а конденсатор C замыкает их на землю, поскольку он обеспечивает незначительное реактивное сопротивление высоких частот.
Таким образом, только низкие частоты ниже частоты среза fc могут проходить без значительного ослабления.
В этом фильтре выходной сигнал снимается через конденсатор C.
Цепь фильтра Т-образного типа
Такая схема фильтра состоит из второго дросселя, подключенного на выходной стороне для улучшения фильтрующего действия.
Такая схема фильтра показана на рис. ниже.
Схема фильтра π-типа
Такая схема фильтра показана на рис. ниже.
Здесь второй конденсатор C2 добавлен в схему для улучшения фильтрующего действия путем заземления более высоких частот.
Катушка индуктивности или дроссель всегда подключаются последовательно между входом и выходом, а конденсаторы заземляются параллельно.
Выходное напряжение снимается на конденсаторе C2.
Фильтр нижних частот — Полезный
Цифровой
Скользящее среднее
EWMA
Экспоненциальная (взвешенная) скользящая средняя (EMA или EWMA) — это название, вероятно, самой простой реализации фильтра нижних частот (первого порядка) для дискретных данных во временной области.
Интуитивно вы создаете выходной сигнал, который медленно следует новым значениям, неявно это означает, что он более вяло реагирует на быстрые изменения (высокочастотный контент), при этом следуя общей тенденции сигнала (низкочастотный контент).
Влияние старых точек данных быстро уменьшается (экспоненциально затухает), хотя оно никогда не достигает нуля (в большинстве компьютерных реализаций это в конечном итоге происходит из-за ошибок округления), что является частью того, почему это (первого порядка ) фильтр с бесконечной импульсной характеристикой (проверить) .
Существует параметр α для изменения его чувствительности.
- В случаях не очень регулярной выборки α связано только со скоростью адаптации к вновь выбранным значениям
- Это по-прежнему актуально для частотного контента, но не особенно поддается количественной оценке
- В приложениях, которые производят выборку с регулярным интервалом, вы можете напрямую связать α с частотным содержанием .
- Например звук. Также например некоторые сенсорные системы, где это необязательно, но иногда этот фильтр может быть более значимым.
Если вы хотите вычислить отфильтрованный выходной ряд из входного ряда, вы можете просмотреть список, выполнив что-то вроде:
filter_output [i] = α * raw_input [i] + (1-α) * filter_output [i-1]
… или эквивалент:
filter_output [i] = filter_output [i-1] + α * (raw_input [i] -filtered_output [i-1])
Последняя форма может показаться более интуитивно понятной / информативной: изменение отфильтрованного вывода пропорционально величине изменения, и , к силе фильтра α.
Оба могут помочь рассмотреть, как использование недавнего отфильтрованного вывода дает системе своего рода инерцию:
- Меньший α (больший 1-α в первом случае) (также способствует большему RC) означает, что выход будет регулироваться более медленно и должен показывать меньше шума (поскольку частота среза ниже (проверьте) ).
- Больший α (меньший 1-α) (меньший RC) означает, что выход будет регулироваться быстрее (иметь меньшую инерцию), но будет более чувствительным к шуму (поскольку частота среза выше (проверить) )
Поскольку вычисление является локальным и однонаправленным, вы можете оставить только последнее значение .Это имеет смысл, например, когда ваша основная цель — представить отфильтрованную версию грубого датчика или шумные влияния
текущий_выход = α * текущий_вход + (1-α) * предыдущий_выход previous_output = current_output
Вы часто хотите реализовать описанное выше в с плавающей запятой , даже если вы возвращаете целые числа, чтобы избежать проблем, вызванных ошибками округления.
- Большая часть проблемы: когда альфа * разница (само по себе плавающее умножение) меньше 1, оно становится 0 в (усеченном) преобразовании в целое число.
- Например, когда альфа равна 0,01, разность сигналов меньше 100 приведет к корректировке на 0 (посредством целочисленного усечения), поэтому фильтр никогда не будет настраиваться на фактическое значение.
- Вы можете сделать это только в int, это требует большей осторожности
Графический пример
Скриншот модифицированного ардуиноскопа. Обратите внимание, что новейших образцов находятся на слева .Верхний сигнал — это необработанный вход.
Ниже приведены его версии EWMA с возрастающей силой.
Некоторые примечания к этому сюжету:
- форма похожа на зарядный конденсатор: пропорциональна разнице, сначала быстро, затем все медленнее и медленнее.
- подавление быстрых пиков и отклонений
- что, конечно, можно слишком сильно фильтровать.
- отфильтрованная версия полнодиапазонного колебания выходит на полпути не столько из-за фильтрации, сколько из-за того, что большинство необработанных отсчетов вокруг них ограничены / насыщены на обоих концах диапазона АЦП.(Это по сути ложный сигнал — клиппинг, т.е. искажение)
По α, τ и частоте среза
α — коэффициент сглаживания, теоретически от 0,0 до 1,0.
На практике обычно <0,2 и часто <0,1 или меньше, потому что выше вы почти не выполняете фильтрацию (или очень медленно сэмплируете).
В DSP это часто основано на:
- Δ t (dt), временной интервал между отсчетами
- выбор постоянной времени τ (тау), а.k.a. RC (проверить)
В частности:
α = dt / (RC + dt)
На практике вы часто выбираете RC, по крайней мере несколько кратных dt, что означает, что α порядка 0,1 или меньше.
При применении к семплам, которые происходят из строгих интервалов (например, для звука),
Отношение RC к частотному содержанию хорошо определено.
Например, частота излома (где она начинает падать, приблизительно частота среза ) составляет:
1 / (2 * пи * RC)
Например, если RC = 0.002сек, колено / отсечка находится на ~ 80 Гц.
При выборке 200 Гц, 2000 Гц и 20000 Гц, что дает альфа-значения 0,7, 0,2 и 0,024 соответственно. (проверить)
Для ФНЧ первого порядка:
- на более низких частотах отклик практически полностью ровный,
- на этой частоте отклик -3дБ (начал снижаться в мягком изгибе / колене)
- на более высоких частотах он падает на 6 дБ / октаву (= 20 дБ / декада)
Обратите внимание, что также будет фазовый сдвиг, который отстает от входного.Это зависит от частоты; он начинается раньше, чем спад амплитуды, и будет составлять -45 градусов на частоте излома (проверить) .
Пример Arduino
Примечание: это версия для одного фрагмента памяти, когда вас интересует только (последнее) выходное значение, например сглаживание зашумленного выходного сигнала датчика.
// сохраняет значения для каждого аналогового вывода, предполагая, что базовый Arduino мультиплексирует 6 контактов.
// вы можете сэкономить несколько байтов памяти, поместив это на контакты с меньшими номерами и понизив...
#define LOWPASS_ANALOG_PIN_AMT 6
float lowpass_prev_out [LOWPASS_ANALOG_PIN_AMT],
lowpass_cur_out [LOWPASS_ANALOG_PIN_AMT];
int lowpass_input [LOWPASS_ANALOG_PIN_AMT];
int adcsample_and_lowpass (int pin, int sample_rate, int samples, float alpha, char use_previous) {
// pin: номер аналогового вывода Arduino для выборки (должен быть 1, если вы хотите более плавных результатов)
// альфа: альфа нижних частот
// use_previous: если true, мы продолжаем регулировку с самого последнего выходного значения.// Если false, мы делаем еще один аналог Прочтите здесь, чтобы заполнить значение.
// При зашумленных сигналах это значение без заправки может вводить в заблуждение,
// и с несколькими выборками на вызов это может не совсем соответствовать реалистичному значению.
// Если вы хотите продолжить со значением, которое мы видели последним, что наиболее актуально, когда
// не ожидается, что значение существенно изменится между вызовами, вы можете использовать true.
// Вам все еще может понадобиться одна начальная выборка, возможно, в setup (), чтобы начать с чего-то реального.
float one_minus_alpha = 1.0-альфа;
int micro_delay = max (100, (1000000 / sample_rate) - 160); // 160 - наша оценка продолжительности цикла
// (~ 110 мкс для аналогового чтения по умолчанию ~ 9 выборок / сек, +50 взято из воздуха (TODO: test)
if (! use_previous) {
// заполняем реальным значением (вместо того, чтобы позволять ему регулировать значение в массивах)
lowpass_input [вывод] = аналоговое чтение (вывод);
lowpass_prev_out [контакт] = lowpass_input [контакт];
}
// Делаем количество сэмплов и lowpass по ходу
int i;
for (i = образцы; i> 0; i--) {
delayMicroseconds (micro_delay);
lowpass_input [вывод] = аналоговое чтение (вывод);
lowpass_cur_out [pin] = альфа * lowpass_input [pin] + one_minus_alpha * lowpass_prev_out [вывод];
lowpass_prev_out [контакт] = lowpass_cur_out [контакт];
}
вернуть lowpass_cur_out [пин];
}
void setup () {
Серийный.begin (115200);
// получаем начальный размер вывода. Предположим, что это может вызвать некоторые странности, поэтому потратьте немного времени
// Занимает примерно 300 мс (300 выборок при примерно 1000 выборок в секунду)
adcsample_and_lowpass (0, 1000, 300, 0,015, ложь); // увидеть ниже
}
void loop () {
// обновления часто могут быть короче (хотя учитывайте максимальную скорость адаптации к большим изменениям)
int result_value = adcsample_and_lowpass (0, // A0
1000, // стремимся к дискретизации 1000 Гц
50, // следим за 50 новыми образцами
0.015, // альфа
правда); // адаптируемся из сохраненного значения для этого пина (устанавливается в setup ())
Serial.println (результирующее_значение);
} 
 Сопротивление – это номинальное значение сопротивления акустики, выражаемое в Ом. Как правило, средним значением является 4 Ом;
Сопротивление – это номинальное значение сопротивления акустики, выражаемое в Ом. Как правило, средним значением является 4 Ом; Существуют несколько порядков кроссовера. В данном случае порядок означает параметр кроссовера, который характеризует его способность ослаблять не нужные частотные сигналы.
Существуют несколько порядков кроссовера. В данном случае порядок означает параметр кроссовера, который характеризует его способность ослаблять не нужные частотные сигналы.
 Это должно быть реализовано так, чтобы до слушателя доходило максимум излучения.
Это должно быть реализовано так, чтобы до слушателя доходило максимум излучения.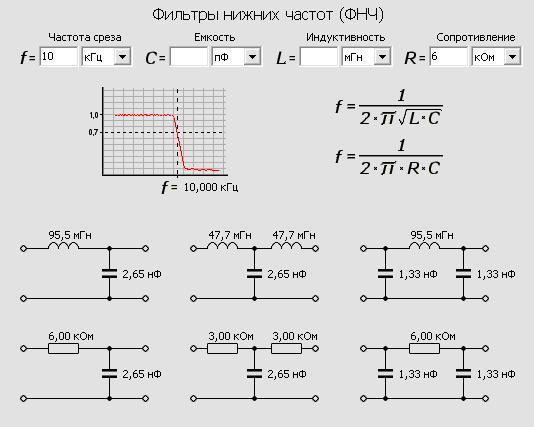 1 мкФ
1 мкФ