Фильтр низких частот простой: Низкочастотный фильтр для сабвуфера

Низкочастотный фильтр для сабвуфера

Приветствую, радиолюбители-самоделкины!

Построение различных звуковых усилителей — популярное направление в радиоэлектронике, об этом говорит как минимум обилие различных схем в интернете. Энтузиасты строят мощные продвинутые Hi-Fi усилители, которые по громкости и качеству превзойдут любой фирменный музыкальный центр, некоторые же ограничиваются созданием более маломощных конструкций, которых достаточно для озвучивания квартиры или комнаты. И если с постройкой самого стерео-усилителя проблем обычно не возникает, благо существуют микросхемы с максимально простыми схемами включения, то вот с постройкой аудиосистем формата 2.1 иногда возникают проблемы с сабвуфером. Нужен он для того, чтобы воспроизводить звуки в нижней части звукового диапазона, обычно от 20 до 100-200Гц, особенно актуально наличие сабвуфера в тех случаях, когда основная акустическая система имеет провал на АЧХ в этой области — а такое часто наблюдается в современной аппаратуре, ведь колонки зачастую ставят в простые пластиковые корпуса без каких-либо расчётов объёма. Сабвуфер представляет собой обычно довольно массивный ящик, как правило из дерева, внутри которого стоит низкочастотный динамик — почти как обычная колонка, вот только объём и внутреннее устройство такого ящика рассчитано именно на максимально эффективное воспроизведение частот в области 20-200Гц. Казалось бы, для сабвуфера можно просто построить дополнительный усилитель и просто подключать его выход к низкочастотному динамика — но такой подход не сработает, так как сперва сигнал нужно обработать — оставить только низкие частоты, срезав всё, что выше 200Гц, для этой цели служит схема специального низкочастотного фильтра. Кроме того, она будет являться предусилителем, в её задачи должны входить регулировка громкости и частоты среза, а также смешивание двух сигналов, правого и левого каналов — в усилителе всего один динамик, моно-усилитель, а потому усиление двух независимых сигналов не требуется, логичнее всего будет их просто смешать, чтобы не терять звук с одного из каналов. Схема такого фильтра представлена ниже.

Как можно увидеть, состоит от из 4-х каскадов а операционных усилителях — можно использовать как 4 микросхемы одинарных операционников (TL071, TL081), так и две микросхемы сдвоенных (TL072, TL082), самый оптимальный вариант — использование одного корпуса микросхемы, внутри которой расположено сразу 4 операционных усилителя — это TL074, именно её и использует автор. Рассмотрим более подробно каждую часть схемы. В левой части находится вход — задействованы как правый, так и левый канал, минус источника сигнала (это может быть плеер или телефон, компьютер) соединяется с минусом схемы. Сразу после входа сигнал попадает на переменные резисторы — их здесь два, но на самом деле это один сдвоенный, служит он для регулировки громкости будущего сабвуфера. Здесь можно использовать практически любой потенциометр на сопротивление около 50 кОм, лучше всего подойдёт с характеристикой логарифмической — громкость будет регулироваться более плавно. Далее сигнал попадает на разделительные конденсаторы С1 и С2, их ёмкость обозначена как 1 мкФ — здесь можно использовать плёночные либо керамические конденсаторы, предпочтение стоит отдать плёночным, так как многие хвалят их за более точную передачу сигнала без искажений, хоть они и более дороги и габаритны. На схеме можно увидеть довольно много конденсаторов небольшой ёмкости, как разделительные между каскадами, так и в цепях обратной связи — для всех них действует данное правило. При повторении схемы желательно точно придерживаться номиналов, ведь они задают частоту среза фильтра, а этом может повлиять на звук. Если в наличии нет резистора или конденсатора нужного номинала, то всегда можно собрать его из двух других путём последовательно или параллельного включения, характеристики при этом не ухудшатся.

На схеме можно увидеть загадочную жирную чёрную вертикальную линию, которая проходит через один из операционных усилителей — так показаны контакты питания. Данная схема требует двухполярного питания, это несколько неудобно, но позволяет операционным усилителям обрабатывать переменный сигнал без добавления дополнительных «костылей» в виде резисторных делителей для получения средней точки питания. Как правило, многие мощные усилители, например, TDA7293, которая как раз может использоваться для усиления сигнала для сабвуфера, также питаются от двухполярного напряжения, поэтому питание можно брать одно и то же. Но с усилителями используется обычно довольно высокое напряжение питания — около 30В на каждое плечо, а то и больше, по этому причине необходимо предусмотреть понижающие стабилизаторы на каждое плечо. Автор для этой цели использовать обычные стабилитроны и резисторы на несколько кОм — в данном случае хороший способ, учитывая, что потребление схемы фильтра достаточно мало и не превышает 20-30 мА. Можно использовать также и стабилизаторы серии 78ХХ на положительное плечо питания и 79ХХ — на отрицательное, подойдут даже в корпусе ТО-92, как и стабилитроны, они не займут много места, но будут более надёжны. Напряжение питания схемы может варьироваться в пределах 9-15В.

Также на схеме можно увидеть ещё один сдвоенный переменный резистор, тем же номиналом в 50 кОм — он служит уже для регулировки частоты среза фильтра. Частоту среза необходимо подобрать уже после сборки фильтра, усилителя и самого корпуса сабвуфера, подбирает просто на слух, по наиболее приятному звучанию. Надписью «SUB OUT» на схеме подписан выход — он будет подключаться ко входу мощного усилителя, минус усилителя при этом соединится с минусом схемы фильтра. Обратите внимание, что выход не содержит разделительного конденсатора, так как усилители обычно имеют его входе, если он будет ещё и на выходе фильтра — то конденсаторы получатся включенными последовательно, что приведёт к уменьшению их общей ёмкости.



Собирается схема на небольшой печатной плате, рисунок которой можно найти в архиве в конце статьи, файл открывается в программе Sprint Layout. Плата содержит все необходимые подписи — к ней на проводах будут подключаться выход, три провода для питания (плюс, минус, земля), а также три канала для входа аудио-сигнала (правый, левый, земля). Подключение аудиосигнала на вход и выход схемы необходимо производить экранированными проводами — иначе не избежать постороннего шума в динамике, идеальным вариантов будет расположение платы фильтра непосредственно около платы усилителя.

Выполняется плата методом ЛУТ, отзеркаливать перед печатью её не нужно. Краткое руководство по ЛУТ методу: сперва вырезается нужный по размеру отрезок текстолита (можно взять немного побольше и предусмотреть места для винтов крепления платы), зашкуривается, откладывается в сторонку. После этого рисунок из программы Sprint Layout печатается на лазерном принтере на глянцевой бумаге. Затем рисунок с бумаги переносится на подготовленную поверхность текстолита, сделать это проще всего утюгом, нагревая бумагу с приложенным текстолитом в течение 1-2 минут. Теперь осталось лишь вытравить лишнюю медь в растворе, например, хлорного железа, просверлить отверстия в плате сверлом 0,8 — 1 мм, залудить дорожки — плата готова для запайки деталей. Монтаж также не представляет ничего сложного в соответствии со схемой — особое внимание стоит уделить полярности электролитических конденсаторов.



Получившуюся плату обязательно нужно отмыть от остатков флюса, проверить правильность монтажа и отсутствие замыканий хотя бы визуально. Теперь можно подключать к плате провода и проверять работоспособность — если под рукой ещё нет усилителя и готового сабвуфера, можно для проверки просто подключить на выход схемы наушники, а на вход подать музыку с телефона — должны быть слышны только низкий частоты, оба потенциометра должны корректно работать. Использовать данную схему можно с любым усилителем и любым сабвуфером — она универсальна. Удачной сборки!
Источник (Source)

Фильтр высоких частот (ФВЧ) и фильтр низких частот (ФНЧ/LPF) в ламповом усилителе

Очень хотелось перейти к теме ламповых усилителей, их простой и увлекательной схемотехнике, особенностям окружения для них и прочим моментам, но я понял, что если начать рассказ сразу с какого то интересного, но произвольного момента, то без некоторых теоретических знаний читатель может не повысить грамотность, а все так же тыкать палкой дохлую белку (менять конденсаторы и резисторы методом тыка), в надежде, что белка оживет.

Если посмотреть на многие схемы ламповых усилителей, то  глаз без труда увидит цепочки фильтров. Они могут образовываться там, где начинающий разработчик о них и не помышлял, это же касается и местной обратной связи.

Поэтому сегодня генеральная репетиция перед основным вхождением в тему лампового усиления – будем разбираться с фильтрами.

В схемотехнике часто применяется фильтр низких частот и фильт высоких частот. Эта тема уже понималась в материалах по ЦАП на сайте, но там была своя специфика.

Первое – название фильтра не то, чем кажется.

Например, ФИЛЬТР НИЗКИХ ЧАСТОТ  занимется тем, что… обрезает ВЫСОКИЕ ЧАСТОТЫ.

Или другими словами, он пропускает низкие частоты до определенной частоты,  выше которой – все, проход закрыт. По английски этот фильтр называется более вразумительно – LPF – Low Pass Filter – фильтр пропускающий низкие частоты.

Т.е.  если в вашей схеме нужно ограничить частотный диапазон по верхнему краю, например от 0 до 35000 гц, то вам нужен фильтр Низких Частот (ФНЧ), который вы настроите на граничную частоту в 35000 Гц.

Другая ситуация, когда вы хотите отрезать низкие частоты – тогда вам нужно использовать Фильтр Высоких Частот (ФВЧ).

ФВЧ пропускает все частоты от нижней заданной частоты и выше.

Например, нужно чтобы диапазон частот устройства начинался с 20 Гц и далее.

Вам нужен ФВЧ фильтр, который отрежет все нижние чатсоты от 0 до Гц, а все что выше 20 Гц не тронет.

Фильт высоких частот и низких  образуется на схеме из связки резистор и конденсатор, что связано с особенностями реагирования элементов на определенные частоты.

В фильтре высоких частот сперва стоит конденсатор, а затем резистор, смотрите картинку.

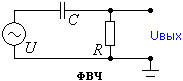
напомню, в ФВЧ вы указываете, что срезать все, что ниже указанной частоты среза. Например 20 гц, и все что ниже не пройдет, а все что выше 20 гц – пройдет. Т.е. вы срезаете “низы” фильтром высоких частот.

Фильтр низких частот (ФНЧ) так же состоит только из резистора и конденсатора, но они меняются местами, смотрите картинку ниже:

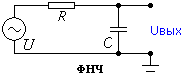
И соответственно вы задаете верхнюю границу среза, т.е. срезаете “верха”, а все что ниже – остается. Например вы задаете 35 кГц, и все что выше – не пройдет, а все что ниже – останется.

Ну и логично, что чтобы ограничить диапазон устройства параметрами 20 Гц – 20 кГц понадобится использовать оба фильтра порезав частоты и сверху (ФНЧ) и снизу (ФВЧ).

Для простоты запоминания – ФНЧ – срезает “верха”, ФВЧ – срезает “низы”.

Такая вверх тормашками логика.

Теперь используем немного математики, чтобы определить, какие номиналы резастора и конденсатора нужны, чтобы получить необходимую частоту среза.

Так как в схемах ламповых усилителей вы чаще всего увидите фильтры высоких частот, то давайте посмотрим на какую-то подобную схему и определим, на какой частоте срез задал неизвестный нам автор схемы (схема взята из интернет).

Честно, чтобы подобрать схему для демонстрации примера мне пришлось потратить время, ибо в 9 из 10 случаев авторы схем, как я понял, вообще не понимали смысл используемых номиналов и значения фильтра были просто бредовый.

Посмотрите внимательно на кусочек схемы, видите ли в

Фильтр низких частот (AD823) для ЦАП TDA1543. Зачем он – hifi-audio.ru

Это продолжение серии материалов про самостоятельное конструирование ЦАП на low cast чипе TDA1543. Ранее были рассмотрены вариации SPDIF-трансиверов на DIR9001, wm8805, CS8412 и тд, были освещены вопросы касаемо TTL-логики и тд.

74HC164

Сегодня мы рассмотрим тему с другого конца. Допустим вы уже реализовали в вашем устройстве цифровой вход, гальваническую развязку, точную клок-генерацию (будет рассказано в отдельном материале). Цап получил цифровую информацию и преобразовал ее в аналоговый сигнал.

Остается преобразовать ток в напряжение и отфильтровать. Тему преобразования тока в напряжения (через сопртивление или активный элемент) мы пока затрагивать не будем, она требует большого материала в будущем, как и не станем глубоко погружаться (пока) в принципы функционирования операционных усилителей.

Тема сегодняшнего обзора – фильтры в цап, что это такое, для чего они нужны и что если без них.

Когда после цап мы преобразовали ток в напряжение (звук) и усилили его до значений необходимых входу интегрального усилителя (стандартно 2 вольта, но может быть в диапазоне от 1 до 3,5 вольт) кажется что все, больше ничего не надо.

В реальности желательно чтобы на усилитель подался только сигнал, который необходимо усилить, а не высокочастотные или низкочастотные помехи возникшие в следствии ошибок (шумов квантования) или помех на линии. Для это используют фильтр оставляющий только заданный диапазон частот.

Бывают фильтры высоких частот и фильтры низких частот. Но здесь, как всегда, все через жопу, читай “трудности перевода”.

Так называемый фильтр низких частот, судя по названию отрезает низкие частоты.

Неправильно.

По английски он пишется как LPF – low-pass filter. Сегодня любой школьник в состоянии это правильно перевести, а именно ФИЛЬТР ПРОПУСКАЮЩИЙ НИЗКИЕ или фильтр пропускающий все, что ниже заданной частоты.

Короче, под ФНЧ (фильтр низких частот) имеется совсем другой смысл, а именно то, что низкие частоты как раз остаются, а срезаются верхние.

Опять же “низкие частоты” понятие относительное. Поэтому воспринимаем все это иначе, а именно:

Все что будет выше указанной частоты будет отрезано.

Если мы настроим ФНЧ на частоту 20000 Гц, то все что ниже этой частоты останется, а все что выше из сигнала будет убрано.

Собственно это то, что нам и надо. Не нравится стандартные 20 кГц, сделайте фильтр на 30, 35 кГц, как хотите. Фильтр все равно будет называться фильтром низких частот.

Реализация фильтра – это конечно практика с математикой, но до вас уже все сделали и рассчитали, есть фильтры Чебышева, Баттерворта и тд.

Эти фильтры отличаются рядом параметров и насколько сильно и круто фильтр сразу срезает. В этом плане самый простой и слабый фильтр первого порядка, больше -6 дБ на октаву не срежет, поэтому применяют фильтры больших порядков. Обычно 2-го порядка, ибо 3-го уже довольно сложен в реализации и практически избыточен в аудио. Но никто не мешает вам реализовать и фильтр 5-го порядка, было бы желание.

Для наших аудио целей лучшим по характеристикам является фильтр Баттерворта 2-го порядка, который и используется в ЦАПах чаще всего, потому что проектируется так, чтобы его АЧХ была максимально гладкой на частотах полосы пропускания.

Я приведу выдержку из википедии о преимуществах этого фильтра:

АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления. При отображении частотного отклика фильтра Баттерворта на логарифмической АФЧХ, амплитуда снижается к минус бесконечности на частотах полосы подавления. В случае фильтра первого порядка АЧХ затухает со скоростью −6 децибел на октаву (-20 децибел на декаду) (на самом деле все фильтры первого порядка независимо от типа идентичны и имеют одинаковый частотный отклик). Для фильтра Баттерворта второго порядка АЧХ затухает на −12 дБ на октаву, для фильтра третьего порядка — на −18 дБ и так далее. АЧХ фильтра Баттерворта — монотонно убывающая функция частоты.

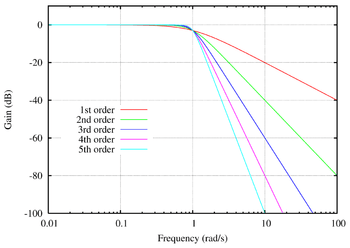
ЛАЧХ для фильтров Баттерворта.

Конечно ваше право не верить, что фильтр Баттерворта хорош, поэтому давайте посмотрим сами его сравнение с другими фильтрами наглядно.

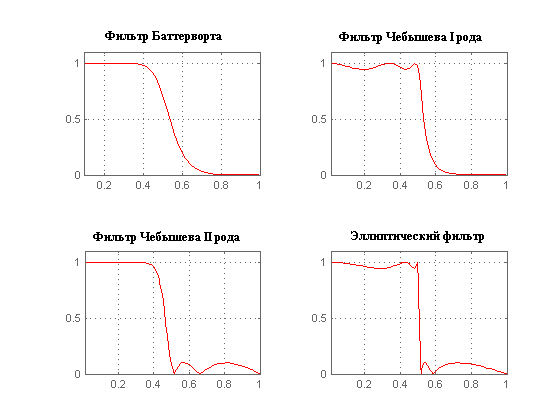
Как видим фильтр Баттерворта получается самый оптимальный по большинству характеристик.

Когда вы станете думать как реализовать математические выкладки в виде радиоэлементов, то обнаружите популярную схему Баттерворта 2-го порядка названную ФНЧ Саллена-Кея.

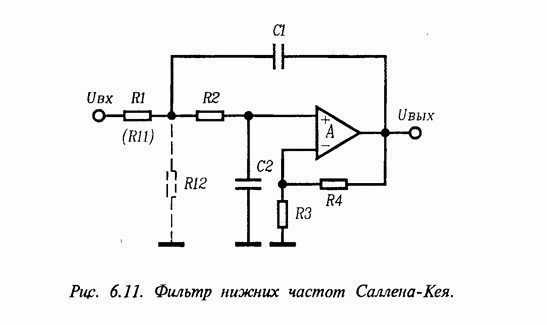
Как рассчитать элементы в этой схеме есть информация в сети, например по этой ссылке рассчет.

Но прежде чем мы перейдем к расчеты схемы фильтра нижних частот на основе активного элемента, а именно ОУ (а фильтр НЧ в такой реализации ничто иное как усилитель напряжение с дополнительным конденсатором включенным в схему для получения нужной АЧХ), я расскажу, что существует еще и фильтр высоких частот.

И аналогично – это черезжопный перевод HPF  – High Pass Filter – фильтр пропускающий высокие частоты, точнее пропускающий все что выше заданной частоты.

Как с этим работать.

Смотрите, у нас есть ФНЧ (Low-pass-filter), который пропускает все что ниже, пусть, 30000 Гц и отрезает весь мусор, что выше 30000 Гц.

Т.е. у нас диапазон воспроизводимых частот сейчас от 0 до 30000 Гц.

Обратите внимание, что для компакт дисков обычно указывают, что  на них записан музыкальный диапазон от 20–20000 Гц. Т.е. На записи нет ничего ниже 20 Гц и выше 20000 Гц.

Кстати, поправьте в чем я заблуждаюсь, ибо непонятно, частота дискретизации СД составляет 44100 Гц, соответственно по теореме Котельникова/Найквиста  следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если наивысшая частота полезного сигнала равна половине или меньше частоты дискретизации (в англоязычной литературе под обозначением половины частоты дискретизации употребляют термин частота Найквиста).

Следовательно верхний диапазон CDDA должен быть 44100/2=22050 Гц, а не 20000.

Но вобщем то не об этом речь.

В случае с исходником на компакт диске, нет смысла использовать ФВЧ (фильтр высоких частот – совершенно неправильный по смыслу термин!) ибо ниже 20 Гц на записи все равно ничего нет.

Так зачем может понадобится ФВЧ?

Если посмотреть на усилители 70х-80х годов, когда одним из популярных источников звука являлся проигрыватель виниловых пластинок, то вы увидите почти на каждом кнопочку срезающую все частоты, что находятся ниже 15 Гц. Это, как вы догадались фильтр ФВЧ.

Зачем он там нужен был?

На пластинках помимо полезного музыкального сигнала присутствовал низкочастотный рокот, гул массы винила, шум детонации, треск царапин об иглу на поверхности пластинки – многие эти паразитные звуки лежали в диапазоне ниже 15 Гц и даже не улавливались ухом, но!

Они улавливались динамиками, отчего казалось бы при отсутствии звука дифузор дергался как сумасшедший – не о какой точности воспроизведения в таких условиях речи уже не шло, как вы воспроизведете легкое колебание, если дифузор шатает низкочастотное колебание как пьяного.

Поэтому вы такой кнопочкой ФВЧ фильтра отрезали все что ниже 15 Гц и радовались звуку без паразитных составляющих. Кроме того самому усилителю значительно лучшало, ибо ему становилось не нужным усиливать эти очень затратные по усилению субнизкие паразитные частоты.

Для чего ФВЧ фильтр может понадобится сегодня. Если вы слушаете только цифровые копии с СД или SACD, то не нужен.

А вот если в вашей коллекции есть оцифровки с винила (с его рокотом и детонацией) или катушечного магнитофона, то хорошо когда такой фильтр предусмотрен в ЦАП.

Но вернемся к более актуальному для большинства ФНЧ-фильтру.

Для цап на TDA1543 я предположил использовать для ФНЧ ОУ компании ADI AD823.

Это двойное ОУ, т.е. я могу реализовать с помощью одного чипа ФНЧ сразу для левого и правого канала.

Это ОУ (AD823) так же интересно тем, что может питаться от однополярного питания (3-36 вольт), а значит при разработке ЦАП можно все элементы записать от единого источника питания +5 вольт, ибо TDA1543, 74HC, CS8414, TCXO 0.1ppm и AD823 требуют одного и того же питания +5v.

К тому же ОУ AD823 довольно быстрая микросхема со скоростью 22 вольта в микросекунду. Для сравнения NE5532 имеет быстродействие лишь 9v в микросекунду.

Итак мы будем использовать AD823, как ФНЧ фильтр и логично, что это будет фильтр Баттерворта 2-го порядка.

К счастью вам даже не нужно особо думать над схемой, ибо схема ФНЧ Баттерворта 2-го порядка сразу и приведена в даташите к операционному усилителю.

Вот она:

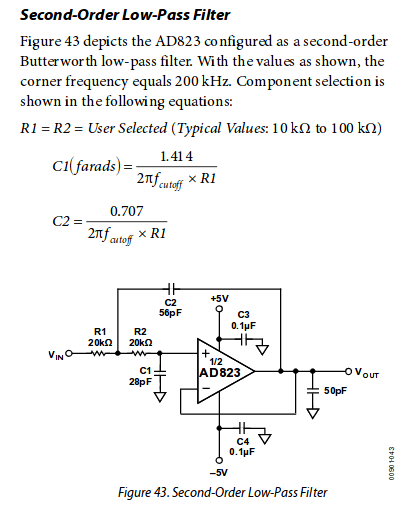
Один нюанс, значение радиодеталей (резисторы и конденсаторы) рассчитаны на частоту 200,000 Гц.

Но выше приведены формулы.

Мы знаем утверждение, что R1= R2, при этом значение R должно быть в диапазоне  от 10 кОм до 100кОм.

Зададим какое то произвольное значение резистора, пусть 47кОм.

Зададим частоту среза Fcutoff, выше которой все будет отрезано, пусть это будет 30000 Гц.

Считаем значение резистора С1.

С1= 1.414/(2*Pi*Fcutoff*R1)

1.414 – это уже посчитанный корень из 2. Для большей точности можно поставить все число 1,414213562.

Если вы выпремляли ток делая из переменного постоянный, то с 1,4142 вы прекрасно знакомы.

Это число 1,414 делим на произведение 2 Пи.

2*Пи=2 * 3,14=6,28

умножаем на желаемую частоту среза, а в нашем случае 30000 Гц

6,28*30000=188400

и умножаем на значение резистора R1. Мы с вами произвольно выбрали из существующих номиналов в диапазоне от 10к до 100к значение 47к.

Умножем 188400*47000=8854800000

Напомню 47 Ком – это 47000 Ом

получим 1,4142/8854800000= 1,59687401183539E-10

Только не пытайтесь делить обычным программным калькулятором, он таких цифр не умеет.

Воспользуйтесь электронной таблицей в OpenOffice или Exel для рассчетов.

Не пугайтесь такого страшного числа, помните, что искомое С задано в Фарадах, чудовищно большой единице.

Чтобы преобразовать ее в пикофарады надо умножить на 1000000000000 (12 нулей), получим

159 pF.

Такого значения у конденсаторов нет, возьмем ближайший в ряду, это 150pF.

Чтобы рассчитать значение С2 нужно воспользоваться формулой

С2= 1.707/(2*Pi*Fcutoff*R2)

Но прежде чем вы не погрузились в вычисления – выдыхайте.

R1=R2, следовательн

Фильтр низкой частоты для сабвуфера

Фильтр низкой частоты для сабвуфера выполнен на распространенных операционных усилителях (LM324, LM358). Неотфильтрованный сигнал подается по двум каналам (правый и левый), а в дальнейшем суммируется, фильтруется и поступает на один выход фильтра.

Особенностью схемы фильтра низкой частоты является его балансный вход, который позволяет подключить источники звука как с дифференциальным выходом (трехпроводным каналом), так и с классическим выходом (двухпроводным). Также есть возможность включения фильтра как после предварительного усилителя, так и после усилителя мощности звуковой частоты (УМЗЧ), в таком случае на входе схемы сигнал ослабляется резисторами.

Фильтру для сабвуфера придают универсальность широкий диапазон напряжения питания, а также ручки регулировки частоты среза ФНЧ, сдвига угла фазы сигнала и коэффициента усиления.

Основные характеристики фильтра низкой частоты для сабвуфера

Напряжение питания Uпит (DC) …… 3…30В

Ток, потребляемый схемой ….. 50мА

Входное напряжение ….. 0…Uпит

Полоса пропускания ….. 20…250Гц

Нижняя частота среза ….. 20Гц-25Гц-30Гц

Верхняя частота среза ….. 30…250Гц

Коэффициент усиления ….. -20дБ…+20дБ

Регулировка фазы ….. 0…360 градусов

Схема фильтра низкой частоты для сабвуфера

Эту схему можно встретить практически среди всех производителей и распространителей наборов для самостоятельной сборки, собственно, откуда она и была взята.

Резисторы R1-R4 ослабляют сигнал, если он подан с выхода усилителя мощности звуковой частоты.

Балансные блоки выполнены на операционных усилителях (ОУ) U1.1-U1.2 и U1.3-U1.4, которые включены как повторители напряжения с единичным коэффициентом усиления, усиливая сигнал по току. ОУ U2.1 представляет собой сумматор.

Сигнал с выхода сумматора поступает на фильтр верхних частот C5, C7, C8, R23, R25, R26, U2.3, который срезает сигнал в области инфранизких частот. Частота среза будет зависеть от подключенного перемычкой XP1 резистора R23, R25 или R26 и равняться 30Гц, 25Гц или 20Гц.

Далее сигнал поступает на фильтр нижних частот, главным образом состоящий из ОУ U2.4 и его пассивных элементов. Изменяя сопротивление резистора R19, плавно изменяется частота среза в диапазоне 30-250Гц.

Таким образом, образуется изменяемая полоса пропускания, которая будет находиться в диапазон 20Гц-250Гц.

Вращая ручку потенциометра R16, происходит  изменение коэффициента усиления, а также изменение угла фазы сигнала. Когда ручка R16 в среднем положении, коэффициент усиления равен -20дБ. В крайних положениях коэффициент усиления равен +20дБ, а угол фазы 0 градусов и 180 градусов соответственно.

Фазовращатель U3.1 позволяет повернуть фазу еще на угол 0-180 градусов.

Регулирование угла фазы позволяет правильно настроить акустическую систему в целом, так как активные фильтры всегда изменяют угол фазы, а в УМЗЧ без фильтров данного эффекта не происходит.

Резистивный делитель R33 и R34 создает среднюю точку питания.

Компоненты схемы фильтра низкой частоты для сабвуфера

При прослушивании музыкальной программы на сабвуфере (тем более в автомобиле) тяжело судить о качестве усиления и о наличии каких-либо искажений. Поэтому, нет необходимости применять дорогостоящие ОУ или пленочные конденсаторы.

Все конденсаторы керамические, за исключением полярных электролитических конденсаторов C14 и C17. Резисторы мощностью 0.25Вт.

Емкости C1-C4 и C18 могут быть как электролитическими полярными, так и неполярными керамическими или пленочными.

В качестве ОУ U1 и U2 можно применить LM324, LM124, MC3403, LM2902, а в качестве U3 можно применить LM358, LM258 или LM2904.

Подключение фильтра низкой частоты для сабвуфера

Подключение фильтра будет зависеть от источника сигнала. Во-первых, это может быть неусиленный (слаботочный) сигнал со звуковой карты или предварительного усилителя. Во-вторых, сигнал на вход фильтра низкой частоты можно подать уже усиленным УМЗЧ. Также, в первом и во втором случае выходы могут быть балансными, это очень редкий случай, но все же.

Когда на вход фильтра подключается неусиленный сигнал по двухпроводной линии (сигнал и земля), то сигнальные провода нужно подключать на X1 (левую) и X3 (правую) клеммы, а клеммы X5 и X7 нужно соединить с минусом питания. Земли сигнальных проводов (правого и левого канала) также нужно соединить с минусом питания.

Если подключение происходит от УМЗЧ, то левый канал подается на X2, правый на X4, а клеммы X5 и X7 необходимо также как и в предыдущем варианте соединить с минусом питания.

Подключая источник с неусиленным дифференциальным выходом (балансный), левый канал — X1 и X5, правый канал — X3 и X7.

Дифференциальный усиленный сигнал подается на клеммы X2 и X6 — левый канал, X4 и X8 — правый канал.

Печатная плата

Печатная плата фильтра низкой частоты для сабвуфера разведена по оригинальной плате из конструктора, идущей в комплекте для самостоятельной сборки. Разведена она не мной. На ней имеются несколько элементов, которые не нужно устанавливать. Я их отметил желтым цветом. Эти элементы совместно с U3.2 образуют генератор прямоугольных импульсов для светодиода. Светодиод мигает, сигнализируя о работе фильтра низкой частоты. Кстати, в комплекте конструктора и на схеме, приложенной к нему, эти элементы отсутствуют. Я собрал сначала с ними, мигающий светодиод раздражает, а в акустической системе слышны помехи. После чего я эти элементы демонтировал.

Размеры печатной платы 100×40мм.

Рекомендации по сборке фильтра низкой частоты для сабвуфера

В первую очередь необходимо установить на плату все семь перемычек. После чего выполняется монтаж остальных компонентов.

После выполнения пайки нужно в обязательном порядке смыть остатки флюса или канифоли, иначе фильтр низкой частоты будет иметь серьезные искажения или вовсе будет работать неисправно.

Также хочу заострить внимание на заземление корпусов переменных резисторов. Настоятельно рекомендую соединить все три корпуса медным проводом и припаять его к отрицательному выводу питания. Если этого не сделать, то в акустической системе будет слышен значительный фон, особенно при касании потенциометров рукой.

Печатная плата фильтра низкой частоты для сабвуфера СКАЧАТЬ

Похожие статьи

Операционные усилители (на основе простейших примеров): часть 3 / Хабр

Краткое введение

Продолжаю спамить писать на тему операционных усилителей. В этой статье постараюсь дать обзор одной из важнейших тем, связанной с ОУ. Итак, добро пожаловать, активные фильтры.

Обзор темы

Возможно, Вы уже сталкивались с моделями RC-, LC- и RLC-фильтров. Они вполне подходят для большинства задач. Но для некоторых целей очень важно иметь фильтры с более плоскими характеристиками в полосе пропускания и более крутыми склонами. Вот тут нам и нужны активные фильтры.
Для освежения в памяти, напомню, какие бывают фильтры:
Фильтр Нижних Частот (ФНЧ) — пропускает сигнал, который ниже определенной частоты (ее еще именуют частотой среза). Википедия
Фильтр Высоких Частот (ФВЧ) — пропускает сигнал выше частоты среза. Википедия
Полосовой Фильтр — пропускает только определенный диапазон частот. Википедия
Режекторный Фильтр — задерживает только определенный диапазон частот. Википедия
Ну еще немного лирики. Посмотрите на амплитудно-частотную характеристику (АЧХ) ФВЧ. На этом графике ничего интересного пока не ищите, а просто обратите внимание на участки и их названия:

Самые банальные примеры активных фильтров можно подсмотреть здесь в разделе «Интеграторы и дифференциаторы». Но в данной статье эти схемы трогать не будем, т.к. они не очень эффективны.

Выбираем фильтр

Предположим, что Вы уже определились с частотой, которую хотите фильтровать. Теперь нужно определиться с типом фильтра. Точнее нужно выбрать его характеристику. Иными словами, как фильтр будет себя «вести».
Основными характеристиками являются:
Фильтр Баттерворда — обладает самой плоской характеристикой в полосе пропускания, но имеет плавный спад.
Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
Фильтр Бесселя — имеет хорошую фазочастотную характеристику и вполне «приличный» спад. Считается лучшим выбором, если нет специфического задания.

Еще немного информации

Предположим, и с этим заданием вы справились. И теперь можно смело приступить к расчетам.
Есть несколько методов расчета. Не будем усложнять и воспользуемся самым простым. А самый простой — это «табличный» метод. Таблицы можно найти в соответствующей литературе. Чтобы Вы долго не искали, приведу из Хоровица и Хилла «Искусство Схемотехники».
Для ФНЧ:

Скажем так, это все Вы могли бы найти и прочитать и в литературе. Перейдем конкретно к проектированию фильтров.

Расчет

В данном разделе попытаюсь кратко «пробежаться» по всем типам фильтров.
Итак, задание # 1. Построить фильтр низких частот второго порядка с частотой среза 150 Гц по характеристике Баттерворда.
Приступим. Если мы имеем фильтр n-ного четного порядка, это означает, что в нем будет n/2 операционников. В данном задании — один.
Схема ФНЧ:

Для данного типа расчета берется во внимание, что R1 = R2, C1 = C2.
Смотрим в табличку. Видим, что К = 1.586. Это нам пригодится чуть позже.
Для фильтра низких частот справедливо:
, где, разумеется,
— это частота среза.
Сделав подсчет, получаем . Теперь займемся подбором элементов. С ОУ определились — «идеальный» в количестве 1 шт. Из предыдущего равенства можно предположить, что нам не принципиально, какой элемент выбирать «первым». Начнем с резистора. Лучше всего, чтоб его значение сопротивления были в пределах от 2кОм до 500кОм. На глаз, пусть он будет 11 кОм. Соответственно, емкость конденсатора станет равной 0.1 мкФ. Для резисторов обратной связи значение R берем произвольно. Я обычно беру 10 кОм. Тогда, для верхнего значение К возьмем из таблицы. Следовательно, нижний будет иметь значение сопротивления R = 10 кОм, а верхний 5.8 кОм.
Соберем и промоделируем АЧХ.

Задание # 2. Построить фильтр высоких частот четвертого порядка с частотой среза 800 Гц по характеристике Бесселя.
Решаем. Раз фильтр четвертого порядка, то в схеме будет два операционника. Тут все совсем не сложно. Мы просто каскадно включаем 2 схемы ФВЧ.
Сам фильтр выглядит так:

Фильтр же четвертого порядка выглядит:

Теперь расчет. Как видим, для фильтра четвертого порядка у нас аж 2 значения К. Логично, что первое предназначается для первого каскада, второе — для второго. Значения К равны 1.432 и 1.606 соответсвенно. Таблица была для фильтров низких частот (!). Для расчета ФВЧ надо кое-что изменить. Коэффициенты К остаются такими же в любом случае. Для характеристик Бесселя и Чебышева изменяется параметр
— нормирующая частота. Она будет равна теперь:

Для фильтров Чебышева и Бесселя как для нижних частот, так и для высоких справедлива одна и та же формула:

Учтите, что для каждого отдельного каскада придется считать отдельно.
Для первого каскада:

Пусть С = 0.01 мкФ, тогда R = 28.5 кОм. Резисторы обратной связи: нижний, как обычно, 10 кОм; верхний — 840 Ом.
Для второго каскада:

Емкость конденсатора оставим неизменной. Раз С = 0.01 мкФ, то R = 32 кОм.
Строим АЧХ.

Для создания полосового или режекторного типа фильтров можно каскадно соединить ФНЧ и ФВЧ. Но такими типами, зачастую, не пользуются из-за плохих характеристик.
Для полосовых и режекторных фильтров также можно использовать «табличный метод», но тут немного другие характеристики.
Приведу сразу табличку и немного ее объясню. Чтоб сильно не растягивать — значения взяты сразу для полосового фильтра четвертого порядка.

a1 и b1 — расчетные коэффициенты. Q — добротность. Это новый параметр. Чем значение добротности больше — тем более «резким» будет спад. Δf — диапазон пропускаемых частот, причем выборка идет на уровне -3 дБ. Коэффициент α — еще один расчетный коэффициент. Его можно найти используя формулы, которые довольно легко найти в интернете.
Ну ладно, хватит. Теперь рабочее задание.
Задание # 3. Построить полосовой фильтр четвертого порядка по характеристике Баттерворда с центральной частотой 10 кГц, шириной пропускаемых частот 1 кГц и коэффициентом усиления в точке центральной частоты равным 1.
Поехали. Фильтр четвертого порядка. Значит два ОУ. Типовую схему приведу сразу с расчтными элементами.

Для первого фильтра центральная частота определяется как:

Для второго фильтра:

Конкретно в нашем случае, опять же из таблицы, определяем, что добротность Q = 10. Рассчитываем добротность для фильтра. Причем, стоит отметить, что добротность обоих будет равна.

Поправка усиления для области центральной частоты:

Финальная стадия — расчет компонентов.
Пусть конденсатор будет равен 10 нФ. Тогда, для первого фильтра:



В том же порядке, что и (1) находим R22 = R5 = 43.5 кОм, R12 = R4 = 15.4 кОм, R32 = R6 = 54.2 Ом. Только учтите, что для второго фильтра используем
Ну и на последок, АЧХ.

Следующая остановка — полосно-заграждающие фильтры или режекторные.
Тут есть несколько вариаций. Наверное, самый простой — это фильтр Вина-Робинсона (англ. Active Wien-Robinson Filter). Типовая схема — тоже фильтр 4го порядка.

Наше последнее задание.
Задание # 4. Построить режекторный фильтр с центральной частотой 90 Гц, добротностью Q = 2 и коэффициентом усиления в полосе пропускания равным 1.
Прежде всего, произвольно выбираем емкость конденсатора. Допустим, С = 100 нФ.
Определим значение R6 = R7 = R:

Логично, что «играясь» с этими резисторами, мы можем изменять диапазон частот нашего фильтра.
Далее, нам надо определить промежуточные коэффициенты. Находим их через добротность.


Выберем произвольно резистор R2. В данном конкретном случае, лучше всего, чтобы он равнялся 30 кОм.
Теперь можем найти резисторы, которые будут регулировать коэффициент усиления в полосе пропускания.


И на последок, необходимо произвольно выбрать R5 = 2R1. У меня в схеме эти резисторы имеют значение 40 кОм и 20 кОм соответственно.
Собственно, АЧХ:

Практически конец

Кому интересно узнать немного больше, могу посоветовать почитать Хоровица и Хилла «Искусство схемотехники».
Также, D. Johnson «A handbook of active filters».
Википедия
Также, кому не очень нужны расчеты, а нужны именно сами фильтры, могу посоветовать полезный софт
P.S. Добавлю очень полезную ссылку и ее зеркало. За линк спасибо spiritus_sancti

Цифровая фильтрация на ПЛИС – Часть 2 / Хабр

Всем привет!

Это вторая публикация на тему «Цифровая фильтрация на ПЛИС». Вторая часть будет посвящена практической реализации КИХ фильтров на FPGA. В процессе подготовки материала я понял, что она раздуется до небывалых размеров, но делить ее на несколько частей не хочется. Поэтому все тонкости теории и синтеза FIR фильтров будут в одной статье, разбитой на взаимосвязанные разделы. Начну обзор с теоретической части, в частности — расскажу об особенностях и методах расчета коэффициентов фильтров. Подробно рассмотрю создание КИХ фильтров в различных средах — MATLAB, CoreGENERATOR, Vivado HLS. Всех заинтересовавшихся прошу под кат.

Часть 2. КИХ фильтр

Теория

Рассмотрим простой пример реализации FIR фильтров. Как известно, существует два больших класса фильтров — БИХ, с бесконечной импульсной характеристикой и КИХ, с конечной импульсной характеристикой. Остановимся на втором типе: КИХ фильтрах (англ. FIR — «finite impulse response»). КИХ фильтр — это линейный цифровой фильтр, основной особенностью которого является ограниченность во времени его импульсной характеристики, то есть с определенного момента времени она становится равной нулю. Как правило, большинство КИХ фильтров выполнено без обратной связи, поэтому практически все КИХ фильтры — нерекурсивные.

Вот так выглядит реализация КИХ фильтра в общем виде, в частности — на ПЛИС.

Все КИХ-фильтры описываются следующими уравнениями:

где y(n) — выходной сигнал (функция текущего и прошедших значений на входе), x(n) — входное воздействие, h(k) — коэффициенты импульсной характеристики, N — длина фильтра (количество коэффициентов фильтра), H(z) — передаточная характеристика фильтра.

В чем секрет КИХ фильтров?
Самая важная особенность КИХ фильтров заключается в возможности получения точной линейной фазовой характеристики. У читателя возникает закономерный вопрос — «а зачем это надо?». Остановимся на этом моменте подробнее. Сигнал подвергается различным преобразованиям при прохождении через фильтр. В частности, изменяются амплитуда и фаза сигнала в зависимости от частотной характеристики фильтра (амплитудной, АЧХ и фазовой, ФЧХ). Для многочастотных сигналов недопустимо, чтобы при прохождении блоков обработки, фаза сигнала искажалась. Причем, если АЧХ в полосе пропускания сделать практически постоянной не составляет труда, то с ФЧХ возникают проблемы. Для оценки искажений фазы удобно ввести понятия фазовой и групповой задержек.
Фазовая задержка — это величина задержки для каждой из частотных компонент сигнала. Определяется как угол сдвига фазы, деленный на частоту. Групповая задержка — это средняя временная задержка всего многочастотного сигнала. Определяется как производная фазы по частоте. Математически фазовая и групповая задержки записываются следующим образом:

Из формулы для групповой задержки становится очевидно условие линейности ФЧХ фильтра. Если ФЧХ — линейна, то групповая задержка после взятия производной равна константе, то есть постоянна для всех частотных компонент. Логично, что фильтр с нелинейной ФЧХ будет вносить искажения в фазу сигнала.
Таким образом, линейность фазовой характеристики — одна из важнейших особенностей КИХ-фильтров. Остановимся на изучении этого класса фильтров.

КИХ фильтры с линейной ФЧХ

Для обеспечения линейности ФЧХ необходимо выполнение условия симметрии импульсной характеристики (или коэффициентов) фильтра. Проще говоря, КИХ фильтр с линейной ФЧХ — симметричен. Существует 4 типа фильтров, отличающихся четностью порядка фильтра N и типом симметрии (положительная или отрицательная). Например, для фильтров с отрицательной симметрией можно получить сдвиг фазы на 90^o. Такие фильтры используются для проектирования дифференциаторов и преобразования Гильберта. Огибающая импульсной характеристики КИХ фильтра строится по закону ~sin(x)/x независимо от типа фильтра (ФНЧ, ФВЧ, ПФ, РФ, дифференциатор). Для решения практических задач зачастую не приходится задумываться о том, какого типа фильтр выбран. Доказательство условия симметрии коэффициентов приводить не буду, но любопытный читатель может найти его сам в различной литературе, ссылки на которую я привожу в конце статьи.

Проектирование КИХ фильтров

Под «расчетом FIR фильтра» в большинстве случаев понимают поиск его коэффициентов по значениям частотной характеристики. Не могу припомнить случаев, когда решалась бы обратная задача за исключением академического интереса.

При создании нового цифрового КИХ фильтра любой инженер проходит через определенные стадии разработки*:

• Спецификация фильтра. Задается тип фильтра (ФНЧ, ФВЧ, полосовой, режекторный), количество коэффициентов N, требуемая частотная характеристика, с допусками на нелинейность в полосе затухания и полосе пропускания и т. д.
• Вычисление коэффициентов. Любыми доступными способами и средствами вычисляются коэффициенты фильтра, удовлетворяющие спецификации из предыдущего пункта.
• Анализ следствий конечной разрядности. На этом этапе оценивается влияние эффектов квантования на коэффициенты фильтра, промежуточные и выходные данные.
• Реализация. На этой стадии происходит разработка фильтра на доступном языке программирования или реализация фильтра путем создания готовых IP-ядер.

* — этапы разработки могут быть несколько иными, но суть всегда остается та же.

Спецификация фильтра

На этой стадии инженер производит поиск компромиссных решений для реализации требуемого фильтра с нужными параметрами. Их немного, но часто приходится жертвовать одним параметром для достижения требуемых значений по другим величинам.

• Apass — неравномерность в полосе пропускания,
• Astop — уровень затухания в полосе подавления,
• Fpass — граничная частота полосы пропускания,
• Fstop — граничная частота полосы затухания,
• N — порядок фильтра (количество коэффициентов фильтра).

На практике, параметры Apass и Astop задают в децибелах (дБ), а расстояние между Fpass и Fstop выражает ширину полосы перехода фильтра. Логично, что значение Apass должно быть как можно меньше, Apass как можно больше, а отношение Fpass/Fstop в идеале стремится к единице (идеально прямоугольная АЧХ). Количество коэффициентов не зря вносится в спецификацию фильтра. Как будет показано далее, от порядка фильтра N и разрядности коэффициентов зависят параметры частотной характеристики фильтра, а также объем занимаемых ресурсов ПЛИС.

Вычисление коэффициентов фильтра

На эту тему можно написать несколько книг и научных статей, но в рамках данной статьи рассматривать подробно все методы не будем. Существует множество методов расчета коэффициентов фильтра — метод взвешивания оконными функциями, метод частотной выборки, различные оптимальные (по Чебышеву) методы с применением алгоритма Ремеза и т.д. Все методы уникальны по своим особенностям и дают те или иные результаты. Для метода оконного взвешивания негативным проявлением становится эффект Гиббса, вносящий неравномерность и выбросы в частотную характеристику фильтра между рассчитанными точками функции. Бороться с ним можно бесконечно, но на практике вводят допуски по неравномерностям в полосе пропускания и полосе подавления.

Основным методом расчета коэффициентов для многих фильтров является модифицированный алгоритм Ремеза — «Parks-McClellan algorithm». По своей сути это косвенный итерационный метод для нахождения оптимальных значений с Чебышевской характеристикой фильтра. Особенность метода заключается в минимизации ошибки в полосе затухания и пропускания путем Чебышевской аппроксимации импульсной характеристики. Вполне логично, что чем больше количество коэффициентов, тем меньше неравномерность АЧХ и тем она прямоугольнее.
От выбора метода зависит конечный результат, но все они сводятся к одним и тем же целям — минимизации выбросов в полосе пропускания и увеличении «прямоугольности» АЧХ.

Анализ следствий конечной разрядности

Разрядность коэффициентов — главный фактор, от которого зависит вид частотной характеристики. В современных ПЛИС разрядность коэффициентов может быть выбрана любой, но разумные цифры лежат в пределах от 16 до 27 битов. Для высоких порядков фильтра часто требуется обеспечить большой динамический диапазон разрядной сетки, но если этого не удается сделать, рано или поздно начинают проявляться ошибки квантования. Из-за ограниченной разрядности коэффициентов модифицируется частотная характеристика, а в некоторых случаях она искажается настолько сильно, что приходится жертвовать параметрами из частотной спецификации для достижения приемлемого результата. Так или иначе, разрядность представления коэффициентов прямо влияет на максимально возможное затухание Astop. Поэтому при использовании слишком ограниченной разрядной сетки коэффициентов, порой невозможно достичь желаемого подавления даже при огромных порядках фильтра!

Разрядность промежуточных данных и арифметическое переполнение — факторы, от которых также зависит вид частотной характеристики и результат на выходе фильтра. Во многих ПЛИС проблема устраняется использованием аккумуляторов большой разрядности в блоках DSP. Например, в ПЛИС Xilinx 6 и 7 серии в ячейках DSP48E1 используются 48-битные аккумуляторы и перемножители. На следующем рисунке представлен стандартный блок DSP48E1, на котором реализуются КИХ фильтры.

Встроенные DSP блоки современных ПЛИС выполнены таким образом, чтобы максимально удобно проводить задачи ЦОС. В первую очередь — для реализации FIR фильтров.

Реализация

Для реализации простейших фильтров требуется совсем немного логических операций. Основной узел, с помощью которого реализуется FIR фильтр — DSP блок ПЛИС. В этом блоке происходят все математические операции — перемножение входных отсчетов с коэффициентами фильтров, задержка входного сигнала, суммирование данных. Современные узлы DSP содержат предварительный сумматор, поэтому даже операции суммирования для фильтров с симметричной ИХ можно делать внутри этого узла. Помимо DSP блока, фильтру нужна память для хранения коэффициентов (распределенная или блочная). Больше фильтр ничего не использует. На рисунке приведена реализация КИХ фильтра с использованием перемножителей, аккумуляторов, линий задержки и памяти для хранения коэффициентов.

Расчет фильтра в MATLAB

Существует множество приложений, в которых можно проводить расчет фильтра и поиск его коэффициентов. Например, LABView, Scope FIR, FDATool из MATLAB или бесплатного аналога Octave. Пожалуй, самым удобным средством расчета КИХ фильтра является MATLAB. Для запуска средства создания и анализа фильтров необходимо в командном окне среды набрать ключевое слово fdatool. Появится примерно вот такое окно (в зависимости от версии MATLAB оно может иметь чуть иной вид):

Основные параметры задаются в окне Filter Specifications. В зависимости от настроек фильтра в области главного окна могут появляться те или иные параметры.

• Filter Order — определяет порядок фильтра (минимальный или заданный пользователем)**.
• Frequency Specifications — определяет частотные параметры характеристики фильтра.
• Magnitude Specifications — определяет амплитудные параметры характеристики фильтра.
• Density Factor — для типа Equiripple задает сетку точек, по которым происходит аппроксимация АЧХ фильтра.

** — в FDATool порядок фильтра N на единицу больше заданного (если задать N = 7, то утилита рассчитывает 8 коэффициентов)!!!

Response type — тип передаточной характеристики фильтра. В этом поле выбирается любой фильтр, какой только существует в природе, например:

• Lowpass — фильтр нижних частот,
• Raised cosine — фильтр «приподнятого косинуса»,
• Highpass — фильтр верхних частот,
• Bandpass — полосовой фильтр,
• Bandstop — режекторный (заграждающий) фильтр,
• Differentiator — дифференциатор,
• Nyquist — фильтр Найквиста,
• Multiband — многополосный фильтр,
• Hilbert transformer — преобразователь Гильберта,
• Arbitrary magnitude — фильтры с произвольной АЧХ.

и т.д.

Причем, в зависимости от типа фильтра, средство анализа укажет на ограничения по типу фильтра и предложит ввести корректное значение N.

Design Method — выбирается метод проектирования фильтра и его тип (БИХ или КИХ). Для БИХ фильтров доступны варианты:

• Butterworth — фильтры с характеристикой Баттерворта,
• Chebyshev Type I, II — фильтры Чебышева,
• Elliptic — эллиптический фильтр,
• Maximally flat — фильтр с максимально плоской характеристикой в полосе пропускания,

и т. д.

Для КИХ фильтров доступны варианты***:

• Equiripple — фильтр с равномерно пульсирующей АЧХ,
• Least-squares — фильтр по методу наименьших квадратов,
• Window — фильтр с оконным взвешиванием различными функциями****,
• Complex Equiripple — комплексный фильтр с равномерно пульсирующей АЧХ,
• Maximally flat — фильтр с максимально плоской характеристикой в полосе пропускания,

и т.д.

*** — наибольший практический интерес представляют фильтры типа Equiripple и Window.
**** — при выборе этой опции появляется панель доступа к оконным функциям и их параметрам.

Для метода Equiripple производится самый простейший расчет КИХ фильтра по модифицированному алгоритму Ремеза. Пользователь задает параметры из спецификации на фильтр и сразу видит результат. В случае неудовлетворительных результатов можно в любой момент изменить один или несколько параметров фильтра и получить другую частотную характеристику. Расчет проводится до тех пор, пока не получены требуемые характеристики. Если не удалось добиться значений по заданию, то рано или поздно придется жертвовать той или иной величиной из спецификации, либо существенно увеличивать порядок фильтра N.

Для метода Window доступно несколько вариантов оконных функций: Bartlett, Blackman, Blackman-Harris, Chebyshev, Flat Top, Gaussian, Hamming, Hann, Kaiser, Rectangular и т. д., вплоть до пользовательских оконных функций (User-defined). Все эти функции обладают своими особенностями и могут давать различные параметры частотной характеристики КИХ фильтра. Часть оконных функций рассчитывается без параметров, а часть фильтров задается через определенные параметры, влияющие на АЧХ фильтра.
Из всех представленных оконных функций, на мой взгляд, самой удобной является окно Кайзера. Для построения АЧХ требуется задать всего один параметр Beta, который влияет на уровень подавления в полосе затухания и на прямоугольность частотной характеристики.

Слева снизу относительно главной рабочей области средство FDATool содержит дополнительные вкладки, в которых можно указать тип фильтра (дециматор или интерполятор), имя модели для вставки в Simulink, тип и разрядность коэффициентов и входных данных и многое другое. В практических целях самые основные вкладки это Design Filter — в ней происходит расчет фильтра, и Quantinization Parameters — в этой вкладке задается тип и разрядность данных.
На верхней панели находятся кнопки, с помощью которых можно посмотреть АЧХ и ФЧХ фильтра, групповую и фазовую задержку, импульсную и переходную характеристики, карту нулей и полюсов фильтра, рассчитанные коэффициенты и т.д.

Скриншоты рабочей области FDAToolГрафик АЧХ и ФЧХ фильтра:

График импульсной характеристики фильтра:

График диаграммы нулей и полюсов:

Помимо всего этого, FDATool позволяет импортировать и экспортировать модели фильтров и рассчитанные коэффициенты. Например, можно рассчитать фильтр и отправить его модель в Simulink в виде модели на стандартных примитивах. Можно рассчитать коэффициенты и сохранить их в отдельном файле, например, как файл с расширением *.h (header). Файл заголовка *.h с коэффициентами фильтра

/*
 * Discrete-Time FIR Filter (real)
 * -------------------------------
 * Filter Structure  : Direct-Form FIR
 * Filter Length     : 128
 * Stable            : Yes
 * Linear Phase      : Yes (Type 2)
 * Arithmetic        : fixed
 * Numerator         : s16,15 -> [-1 1)
 *   Round Mode      : convergent
 */

/* General type conversion for MATLAB generated C-code  */
#include "tmwtypes.h"

const int BL = 128;
const int16_T B[128] = {
      -18,      0,     19,     39,     58,     75,     88,     97,    100,
       96,     85,     68,     44,     16,    -16,    -50,    -83,   -113,
     -139,   -157,   -166,   -164,   -152,   -128,    -94,    -51,      0,
       55,    111,    164,    211,    248,    272,    280,    269,    240,
      192,    126,     45,    -47,   -146,   -245,   -339,   -421,   -483,
     -521,   -528,   -501,   -434,   -329,   -183,      0,    217,    462,
      728,   1006,   1288,   1564,   1823,   2056,   2254,   2409,   2517,
     2571,   2571,   2517,   2409,   2254,   2056,   1823,   1564,   1288,
     1006,    728,    462,    217,      0,   -183,   -329,   -434,   -501,
     -528,   -521,   -483,   -421,   -339,   -245,   -146,    -47,     45,
      126,    192,    240,    269,    280,    272,    248,    211,    164,
      111,     55,      0,    -51,    -94,   -128,   -152,   -164,   -166,
     -157,   -139,   -113,    -83,    -50,    -16,     16,     44,     68,
       85,     96,    100,     97,     88,     75,     58,     39,     19,
        0,    -18
};

Кроме того, можно создать файл коэффициентов *.COE в специальном формате для Xilinx. Для этого нужно выбрать тип коэффициентов с фиксированной точкой и задать их разрядность. Затем нажать Targets -> Xilinx Coefficient (.COE) File, в результате чего в главном окне MATLAB отобразится содержимое файла — глобальные настройки и коэффициенты в HEX-формате. Пример *.coe файла

; XILINX CORE Generator(tm)Distributed Arithmetic FIR filter coefficient (.COE) File
; Generated by MATLAB(R) 8.3 and the DSP System Toolbox 8.6.
;
; Generated on: 06-Dec-2015 15:35:35
;
Radix = 16; 
Coefficient_Width = 18; 
CoefData = 3ffeb,
00018,
00049,
00067,
0005f,
00029,
3ffd2,
3ff79,
3ff46,
3ff59,
...

Видно, что при подаче на вход единичного импульса, на выходе образуется не что иное, как импульсная характеристика фильтра (график из Simulink).

Xilinx FIR Compiler

Как и в случае с CIC фильтром, приведу подробное описание средства создания FIR фильтров от Xilinx. Отмечу, что описание содержит не просто перевод из даташита, а замечания и рекомендации из личного опыта и опыта моих коллег.

FIR Compiler — Вкладка 1:

Component name — имя компонента (используются латинские буквы a-z, цифры 0-9 и символ «_»).
Рекомендую использовать осмысленные имена, в которых зашифрованы главные параметры фильтра. Например, xfir128t_d1_b18_4c_w6_a7 — фильтр, сделанный для Xilinx, N = 128 (taps), децимация не используется, разрядность коэффициентов 18, четыре канала, применена оконная функция Кайзера с параметром beta = 6, кристалл ПЛИС — Artix-7.

Filter Coefficients:

• Select source — выбор источника коэффициентов (Vector — вектор, заданный вручную или COE File — файл с набором коэффициентов). Предпочтительно использовать перегружаемые *.COE файлы.
• Coefficient Vector — вектор коэффициентов, задаваемый вручную.
• Coefficient File — вектор коэффициентов, считываемый из файла.
• Number of Coefficient Sets — количество реально используемых DSP блоков для обработки коэффициентов. Количество коэффициентов должно делиться нацело на указанное значение. Полезная опция при работе на высокой частоте относительно частоты дискретизации, позволяет существенно экономить ресурсы ПЛИС.
• Number of Coefficient (per set) — количество коэффициентов, обрабатываемых единовременно DSP блоками. Значение в поле автоматически устанавливается при считывании количества коэффициентов и предыдущего параметра.

Filter Specification:

• Filter type — тип фильтра: простой / интерполирующий / децимирующий / полифазный.
• Rate Change Type — изменение скорости обработки. Может быть целочисленным или дробным.
• Interpolation / Decimation Rate Value — коэффициент интерполяции / децимации.
• Zero Pack Factor — для интерполирующих фильтров параметр определяет количество нулей, вставляемых между коэффициентами.
• Number of channels — количество независимых каналов фильтрации: 1-64.

Hardware Oversampling Specification: эти параметры влияют на выходную частоту дискретизации, количество тактов, требуемых для обработки данных. От этих параметров также зависит уровень параллелизма внутри ядра и количество занимаемых ресурсов.

• Select format — выбор частотных соотношений фильтра: Frequency Specification / Sample period.
• Frequency Specification — Частотная спецификация: пользователь задает частоту дискретизации и частоту обработки данных.
• Sample period — Тактовая спецификация: пользователь задает отношение частоты обработки к тактовой частоте данных.
• Input Sampling Frequency — входная частота дискретизации: *.
• Clock frequency — частота обработки фильтра: *****.
• Input Sampling period — отношение частоты обработки к частоте входного тактового сигнала: *****.

***** — диапазон зависит от общих настроек и коэффициента дискретизации R.

FIR Compiler — Вкладка 2:

Filter Architecture — задает реализуемую архитектуру фильтра.

• Systolic Multiply Accumulate — систолический фильтр с накоплением,
• Transpose Multiply Accumulate — перестраиваемый фильтр с накоплением,
• Distributed Arithmetic — фильтр на распределенной логике ПЛИС.

Coefficient Options — параметры для коэффициентов

• Use Reloadable Coeffcients — использовать перегружаемые коэффициенты. Полезная опция для реализации в одном фильтре перегружаемых частотных характеристик.
• Coefficient Structure — структура коэффициентов, 5 типов: несимметричные, симметричные, отрицательно симметричные, полуполосные и с преобразованием Гильберта. По умолчанию FIR compiler пытается сам определить тип коэффициентов (inferred).
• Coefficient Type — тип коэффициентов: знаковый или беззнаковый.
• Quantization — задает метод округления: целочисленные коэффициенты, округление к ближайшему целому или максимальный динамический диапазон (масштабирует коэффициенты относительно максимального).
• Coefficient Width — разрядность коэффициентов. Значение в этом поле влияет на частотную характеристику фильтра, что можно наблюдать в соответствующем окне (Freq. Response).
• Best Precision Fraction Length — автоматически устанавливает наилучшее соотношение для целой и дробной частей разрядной сетки.
• Coefficient Fractional Bits — определяет позицию для разделения целой части от дробной в разрядной сетке представления коэффициентов.

Datapath Options — опции входных данных

• Number of Paths — определяет количество параллельных каналов для обработки. Количество DSP ядер пропорционально значению в этом поле. Для этой опции на вход фильтра поступает несколько независимых потоков данных, в то время как для параметра Number of Channels данные поступают на один вход и обрабатываются последовательно.
• Input Data Type — тип данных на входе фильтра (знаковый или беззнаковый).
• Input Data Width — разрядность входных данных.
• Input Data Fractional Bits — определяет количество бит, приходящихся на дробную часть представления входных данных. Значение в этом поле не влияет на реализацию фильтра! (число с фиксированной точкой можно представить как угодно: с дробной частью или вовсе без нее, но результат один и тот же).
• Output Rounding Mode — режим округления выходных данных: полная точность, отбрасывание младших значащих битов, округление до целого вниз/вверх, округление до четного/нечетного. Во многих задачах не требуется менять этот параметр и можно оставить Full Precision — полную точность.
• Output Width — разрядность выходных данных фильтра.
• Output Fractional Bits — количество бит, определяющих дробную часть выходных данных. Поле информативное и не влияет на реализацию фильтра.
• Allow Rounding Approximation — для режимов Symmetric Rounding Mode опция разрешает аппроксимацию при округлении без дополнительных затрат ресурсов (автоматическое определение знакового бита в слове).
• Registered Output — активная опция добавляет на выход фильтра дополнительный регистр для увеличения производительности (максимальной частоты обработки) фильтра.

FIR Compiler — Вкладка 3:

Optimization Goal — определяет цель оптимизации при создании фильтра (Area — по площади, Speed — по скорости). В большинстве случаев удается одновременно достичь максимальной скорости и минимальной затраты ресурсов, но в специфических случаях при указании Speed фильтр оптимальным образом расставляет внутренние регистры в критических путях между логическими функциями.

• SCLR — синхронный сброс фильтра (логическая единица на входе производит сброс).
• Use Deterministic SCLR Behavior — определяет поведение внутренних данных фильтра типа Multiply-Accumulate в процессе сброса. При активной опции сигнал сброса очищает внутренние регистры, память данных и хранения коэффициентов.
• ND — «New data», входной сигнал, определяющий поступление данных на вход фильтра. Вместе с сигналом RFD позволяют организовать пакетную обработку данных. Как правило, сигналы ND и RFD подключают к управляющим сигналам FIFO.
• CE — «Clock Enable», сигнал разрешения тактирования фильтра. При низком уровне на входе этого сигнала приостанавливается любая обработка внутри фильтра, независимо от того, поступают новые данные или нет.
• DATA_VALID — сигнал валидности выходных данных. Опция полезна только в многоканальном режиме (Number of Channels > 1).

Memory Options — глобальные настройки выбора типа памяти для хранения входных данных, коэффициентов фильтра, промежуточных и выходных данных. Выбирая блочную память вместо распределенной, в некоторых случаях можно в сотни раз сэкономить логические ресурсы ПЛИС!
Для Data / Coefficient / Input / Output Buffer Type возможны режимы Auto / Block / Distributed.
Preference for Other Storage — определяет тип памяти для промежуточных данных. Также доступны режимы Auto / Block / Distributed.

DSP Slice Column Options — определяет настройки распределения DSP блоков между колонками ПЛИС. Для некоторых архитектур фильтров, например, с симметричными коэффициентами недоступен режим Multi-Colomn Support, поэтому необходимо следить за возможной реализацией фильтра.

• Device Column Lengths — определяет длину колонок DSP блоков. Полезное информативное поле, в котором можно заранее определить верхнюю границу порядка фильтра и максимальное количество реализуемых фильтров.
• Column Configuration — определяет конфигурацию и положение DSP блоков в колонках. С этим параметром нужно работать осторожно, поскольку при разрыве фильтра между несколькими колонками может возникнуть большая задержка, следовательно — упадет максимальная тактовая частота.
• Inter-column Pipe Length — определяет количество дополнительных регистров между колонками DSP блоков для устранения негативного эффекта задержки распространения.

FIR Compiler — Вкладка 4:

Summary — эта вкладка в виде списка отражает конечные настройки фильтра (количество каналов, порядок фильтра, параметры частот, разрядность входных, выходных и промежуточных данных, разрядность коэффициентов, задержка в фильтре, количество используемых DSP блоков, наличие сигналов контроля и т.д.).

В левой части окна FIR Compiler есть три полезные дополнительные вкладки:

• IP-symbol — схематичный вид IP-блока с активными портами ввода/вывода.
• Freq. response — частотная характеристика FIR-фильтра.
• Implementation Details — оценка занимаемых ресурсов DSP и RAMB, суммарная задержка, количество коэффициентов и порядок их загрузки.

Абстрактный пример

Условие
Проведем расчет широкополосного фильтра первичной обработки, обладающего следующими параметрами:

• Частота дискретизации Fs: 250 МГц,
• Частота среза фильтра Fpass: 55 МГц,
• Коэффициент прямоугольности: > 0.88 (Fpass/Fstop),
• Подавление в полосе пропускания (Apass): < 0.5 дБ,
• Подавление в полосе затухания (Astop): > 50 дБ.

Реализовать шесть независимых каналов фильтрации на микросхеме Artix-7 XC7A100T-FGG484. Коэффициенты ИХ – перегружаемые, симметричные и независимые для каждого канала фильтра.

Решение

Шаг 1: Оценка ресурсов ПЛИС
Необходимо понять, сколько доступно ресурсов кристалла для реализации подобного фильтра. В DS180 можно найти, что микросхема имеет 240 DSP48E1 блоков, выстроенных в три колонки (это важно!). Из ТЗ известно, что ИХ – симметрична, а это значит, что для фильтра порядка N потребуется N/2 блоков DSP48E1. Следовательно, на выбранной микросхеме возможна реализация 2 фильтров с длиной характеристики N = 240, либо 6 фильтров с длиной N = 80. В практических целях при обработке сигналов длину ИХ выбирают кратному степени двойки. Например, N = 64, 128 или 256. Либо, N = (128 + 64), (32 + 16 + 8). В нашем случае необходимо реализовать 6 фильтров на 240 DSP блоках. С учетом симметрии для каждого фильтра возможно использовать длину N < 81 коэффициентов. Предположим, что для достижения параметров фильтра хватит N = 80 = 64 + 16 коэффициентов.

Шаг 2: Поиск коэффициентов фильтра

Запустим FDATool и внесем в нужные поля параметры фильтра из спецификации (помним, что порядок N задается на 1 меньше, чем истинный порядок фильтра). Режим 1 – Equiripple. Для частоты среза Fpass = 55 МГц и коэффициента прямоугольности > 0.85 найдем частоту заграждения Fstop < 62.5 МГц. На следующем рисунке представлен расчет фильтра по требуемым параметрам:

Как видно, фильтр удовлетворяет всем перечисленным требованиям.
Режим 2 – Window. Неожиданно перед самой сдачей проекта вашему заумному заказчику вбрела в дурную голову мысль. «Хочу 70 дБ подавление при прочих равных условиях!». Элементная база выбрана, плата разведена и смонтирована, ПЛИС установлена, проект отлаживался несколько месяцев и нет возможности поставить что-то переделывать. Что делать? Проектировать свой собственный КИХ фильтр за неделю до сдачи проекта? Искать другие методы подавления АЧХ? Переделывать плату и устанавливать ПЛИС пожирнее? Нереально! Главное – не паниковать. Метод Equiripple уже не спасает. Переходим к оконному режиму Window. При выборе моего любимого окна Кайзера можно добиться лучших характеристик фильтра. Например, обеспечить необходимое подавление в полосе затухания Astop = 80 дБ (параметр Beta = 8). Но для оконного метода следует учитывать, что в полосе затухания из-за недостаточной разрядности коэффициентов могут проявляться эффекты квантования.

Далее известным способом выгружаем рассчитанные коэффициенты в *.COE файл для дальнейшей работы.

Шаг 3: Реализация

Количество каналов и коэффициентов было подобрано таким образом, чтобы на 100% занять ресурсы DSP48E1 в ПЛИС. Количество занимаемых ресурсов для 6 каналов на рисунке ниже:

Не стоит пугаться, что проект не заработает на 250 МГц. Еще как заработает. PlanAhead любит перестраховываться и указывает значения ниже реальных. Результаты разводки шести каналов FIR фильтров.

Красивые рисунки разводки проектаСхематический вид части IP-ядра FIR фильтра:

Разводки платы в FPGA Editor (Zoom нижней части):

Разводка платы в FPGA Editor:

Практические советы

Конечно, переход к Window спасает не всегда, и на практике есть несколько иных методов, которые так или иначе упростят жизнь разработчику.

1. Заранее определить возможную децимацию сигнала (по отношению частоты дискретизации и граничной частоте в спектре сигнала). Использовать дешевые CIC-фильтры для целей децимации. После децимации возможно сократить количество используемых DSP блоков кристалла.
2. Определить отношение частоты дискретизации и частоты обработки в кристалле ПЛИС. Если частота обработки в несколько раз превышает частоту дискретизации, можно во столько же раз сэкономить количество ресурсов на реализацию FIR фильтра.
3. Реализовать фильтр на распределенной логике ПЛИС, если это возможно и не критично с точки зрения частот обработки. Этот метод очень сложен в реализации и не будет стабильно работать для больших порядков фильтра N.
4. Для реализации фильтров с симметричной ИХ предварительно оценить размер колонок DSP блоков и количество этих колонок в ПЛИС. Для реализации длинных фильтров с симметричной ИХ требуется каскадное соединение DSP блоков и при размещении фильтра внутри ПЛИС в одной колонке может не хватить ячеек DSP. С другой стороны, при реализации независимых каналов фильтров, может попросту не хватить колонок, если в каждой колонке умещается только один фильтр. Придется либо уменьшать длину характеристики, либо делать два небольших фильтра с меньшим числом коэффициентов.******
5. Для современных кристаллов ПЛИС (Altera и Xilinx) при реализации фильтра с симметричной ИХ использовать предварительный сумматор в узле DSP, а не на распределенной логике. Внутренний pre-adder значительно экономит не только логические ячейки, но и трассировочные ресурсы кристалла! *******

****** — Для Xilinx фильтр гарантированно не разведется, если фильтр с симметричной ИХ не влезает в одну колонку (в PlanAhead колонки DSP блоков выделены зеленым цветом). На Altera – не проверял. Буду рад, если кто-то поделится своими опытами.
******* — для микросхем ПЛИС фирмы Xilinx 7 серии и старше этот метод спасает только в том случае, если разрядность коэффициентов не превышает 18. Для убер-современных по состоянию на 2015-2016 г. микросхем Xilinx Ultra-Scale возможно реализовать предварительный сумматор с разрядностью коэффициентов 24.

Vivado HLS

Современные методы создания узлов задач цифровой обработки сигналов на ПЛИС сводятся к двум принципам:

• уменьшение времени проектирования (понятие «time-to-market«),
• уменьшение порога вхождения (популяризация ПЛИС среди С++ разработчиков).

Оба принципа возникли не случайно и происходят в первую очередь от постоянного увеличения логической емкости FPGA. Xilinx заявляет, что старые методы программирования (на языках VHDL и Verilog) уже не справляются с современными задачами, и есть большая вероятность, что в будущем программирование на ПЛИС будет вестись исключительно на языках высокого уровня типа С и С++. Xilinx несколько лет назад анонсировал новое средство проектирования под названием Vivado HLS и предлагает все большие проекты частично или полностью переводить на новый уровень. Разработка на Vivado HLS сводится к тому, что можно уйти от понятия «тактовая частота» и разрабатывать сложные алгоритмы без привязки к ПЛИС, а всю оптимизацию под ПЛИС уже делать на последней стадии проекта. Посмотрим, что можно сделать с помощью новой среды и разработаем простейший КИХ-фильтр в Vivado HLS.

В качестве примера я взял одну из лабораторных работ от Xilinx, в которой в первом приближении показана вся мощь современных средств. Основная разработка с помощью Vivado HLS базируется на взаимосвязанных задачах: написание кода и его оптимизация по скорости (Speed) и занимаемой площади (Area) с помощью директив.

Xilinx предлагает следующее поведение при проектировании:

• – C Validation/Simulation (Project -> Run C Simulation): написание алгоритма, отладка проекта, выявление ошибок в коде, сравнение данных с эталоном и т.д.
• – C Synthesis (Solution -> Run C Synthesis): синтез проекта из C-кода в RTL форму и анализ полученных данных: оценка производительности (latency, trip count, speed etc.), оценка ресурсов, полученный интерфейс ввода/вывода.*
• – RTL Verification (Solution -> Run C/RTL Cosimulation): повторное использование C-модели теста main() для анализа RTL-модели (self-checking).
• – IP Creation (Solution -> Export RTL): создание IP-ядра для дальнейшего использования в основном проекте (Xilinx ISE, Vivado и т.д)

* — Мощь Vivado HLS в создании уникальных решений (solutions), различающихся способами оптимизации. Правильный подход заключается в создании множества решений и выборе оптимального, нежели в отладке одного единственного!

Как сделать различные решения? Использовать директивы — инструмент для оптимизации проектов в Vivado HLS. Директивы можно добавлять в исходный код (Source file) или в отдельный файл директив (Directive file).

• Source file – подходит для задания директив, которые НЕ БУДУТ меняться на протяжении создания проекта. Например, директивы для интерфейса портов I/O не меняются. В проекте эти директивы обозначаются префиксом: #HLS.
• Directive file – подходит для задания условий и ограничений, которые влияют на оптимизацию по скорости и размещению. Как правило, в проекте можно сравнить в различных solutions несколько ограничений и выбрать оптимальное. В проекте эти директивы обозначаются префиксом: %HLS.

Приведу пример исходников для простейшего КИХ фильтра. Обратите внимание на директивы в исходном коде.FIR Filter C++ for Vivado HLS

#include "fir.h"

void fir (
  data_t *y,
  coef_t c[N],
  data_t x
  ) {
<b>#pragma HLS</b> INTERFACE ap_ovld port=y
<b>#pragma HLS</b> INTERFACE ap_vld port=x
<b>#pragma HLS</b> RESOURCE variable=c core=RAM_1P_BRAM

  static data_t shift_reg[N];
  acc_t acc;
  data_t data;
  int i;
  
  acc=0;
  Shift_Accum_Loop: for (i=N-1;i>=0;i--) {
		if (i==0) {
			shift_reg[0]=x;
     	data = x;
    } else {
			shift_reg[i]=shift_reg[i-1];
			data = shift_reg[i];
    }
    acc+=data*c[i];;       
  }
  *y=acc;
}

Директивы в отдельном файле выглядят следующим образом:

set_directive_unroll "fir/Shift_Accum_Loop"
set_directive_array_partition -type complete -dim 1 "fir" shift_reg

Замечание: В процессе оптимизации разработчику часто приходится сравнивать различные результаты по производительности и ресурсам. Поэтому зачастую большая часть директив записывается в отдельный файл. Если разработчик уверен, что конкретная оптимизация нужна для всех решений, то её можно занести в исходные тексты!

Для проекта FIR создадим три разных решения:

• без использования директив (синтезатор использует минимум ресурсов — последовательная обработка данных),
• с использованием директив для портов (синтезатор оптимизирует интерфейс ввода/вывода),
• с использованием директивы UNROLL (для разворачивания цикла FOR и параллельной обработки каждой итерации цикла).

В результате синтеза в Vivado можно провести полный анализ по занимаемым ресурсам и максимальной производительности, увидеть интерфейс портов ввода/вывода для создаваемого ядра. Кроме того, можно увидеть, как исполняются те или иные функции, сколько ресурсов они занимают и сколько тактов выполняются.

Сравнение трех решений:

Результаты синтеза проекта в Vivado HLSДирективы:

Вкладка Performance:

Вкладка Resources:

• Чтение порта x и запись порта y происходит за один такт. Чтение порта c за два такта, потому что он описан как интерфейс памяти RAM;
• Используется два умножителя;
• Сдвиговый регистр shift_reg используется для операции чтения и записи;
• Остальные ресурсы не используются совместно, потому что существуют в единственном виде (в выражениях в коде).

Ресурсы кристалла:


Процесс создания нового проекта и все шаги проектирования описывать не буду, поскольку статья и так уже разрослась до небывалых размеров. Но если вам интересна тема использования Vivado HLS в своих проектах – я с удовольствием поделюсь своим опытом. Также можно воспользоваться помощью хабраюзера urock. В этом деле он мастер!

Заключение

На этом хотелось бы подвести итог. В статье рассмотрены базовые принципы создания КИХ фильтров на ПЛИС. Общие выводы по статье:

• КИХ фильтры — линейные нерекурсивные фильтры, достаточно просты в реализации на современных FPGA и процессорах.
• Порядок фильтра = длина импульсной характеристики = количество коэффициентов = количество линий задержки.
• Могут иметь точную линейную фазовую характеристику, постоянные групповую и фазовую задержки.
• Для линейной фазовой характеристики требуются симметричные коэффициенты фильтра.
• Не забывайте про эффект Гиббса при расчете коэффициентов фильтра.
• При расчете коэффициентов пользуйтесь современными средствами и не изобретайте велосипед
• Если длина фильтра N превышает разумные пределы (например, больше 512), используйте алгоритм быстрой свертки через двойное БПФ.
• Разработка фильтра разбивается на несколько взаимосвязанных стадий.
• Используйте метод оконных функций для реализации частотных характеристик с хорошими параметрами.
• Учитывайте особенности выбранного кристалла ПЛИС для минимизации занимаемых ресурсов.
• Длина фильтра влияет на прямоугольность, а разрядность коэффициентов на подавление в полосе затухания.
• Существует множество методов разработки КИХ фильтров на ПЛИС. Выбирайте тот, который покажется проще.

Полезные видеоAltera FIR Design:

Xilinx HLS FIR Design 1:

Xilinx HLS FIR Design 2:

Литература

1. Статья на хабре
2. Статья на DSPLIB
3. Altera FIR Compiler
4. Xilinx FIR Compiler
5. Xilinx DSP48E1 (7 Series)
6. Xilinx DSP48E2 (Ultra-Scale)
7. Wikipedia FIR
8. Parks-McClellan algorithm
9. MATLAB Tutorial 1
10. MATLAB Tutorial 2
11. OpenCores FIR 1
12. OpenCores FIR 2
13. OpenCores FIR 3

Продолжение следует…

Проектирование и расчеты схемы простого LC фильтра нижних частот »Электроника

Конструктивные соображения, схема и формулы для 3-полюсного ЖК-фильтра нижних частот с постоянным k для ВЧ приложений.

---

Фильтр постоянного K Включает:
Фильтр постоянного k Простая конструкция LC LPF Конструкция LC HPF Конструкция полосового фильтра LC

Базовый набор фильтров включает: : RF фильтры — основы Характеристики фильтра Основы проектирования ВЧ-фильтров Конструкция фильтра высоких и низких частот Постоянный k-фильтр Фильтр Баттерворта Фильтр Чебычева Фильтр Бесселя Эллиптический фильтр

---

Часто бывает сложно разработать простой ЖК-фильтр нижних частот, поскольку вычисления могут быть трудными для выполнения или таблицы нормализованных значений могут быть недоступны.

Несмотря на то, что в Интернете есть несколько калькуляторов фильтров, с уравнениями для простого фильтра легко работать, и они дают представление о работе фильтра.

Основы проектирования ФНЧ

Фильтры нижних частот используются в большом количестве приложений. В частности, в радиочастотных приложениях фильтры нижних частот изготавливаются в форме LC с использованием катушек индуктивности и конденсаторов. Обычно они могут использоваться для фильтрации нежелательных сигналов, которые могут присутствовать в полосе частот выше желаемой полосы пропускания.Таким образом, этот вид фильтра принимает только сигналы ниже частоты среза.

Фильтры нижних частот обычно состоят из нескольких секций. Они могут иметь конфигурацию Pi (Π) или T. В фильтре Π секции каждая секция имеет одну последовательную катушку индуктивности и конденсатор на земле с каждой стороны.

Стандартный 3-полюсный Π LC фильтр нижних частот RF

Сетевой фильтр нижних частот T имеет один конденсатор между линией RF и землей, а в сигнальной линии есть две катушки индуктивности, по одному с каждой стороны.Т-образная секция не всегда так удобна, потому что даже при наличии дополнительных секций все равно требуется больше индукторов, которые дороже покупать или требуют отдельной обмотки.

Типовой 3-полюсный T LC фильтр нижних частот RF

Уравнения конструкции фильтра нижних частот

Существует множество различных вариантов фильтров, которые могут использоваться в зависимости от требований с точки зрения пульсации в полосе, скорости, с которой достигается окончательный спад, и т. Д. Используемый здесь тип — константа-k, и это дает некоторые управляемые уравнения. :

L = Z0π fc Генри

C = 1Zo π fc Фарады

fc = 1πL C Гц

Где:
Z ₀ = характеристическое сопротивление в омах
C = емкость в фарадах
L = индуктивность в единицах Генри
f _c = частота среза в герцах

Дополнительные детали конструкции

Есть несколько идей и указателей, которые можно учесть при разработке и реализации конструкции фильтра нижних частот.

• Каскадные секции для большего спада: Чтобы обеспечить больший наклон или спад, можно каскадировать несколько секций фильтра нижних частот. При этом фильтрующие элементы из соседних секций можно комбинировать. Например, если два Т-образных фильтра соединены каскадом, и каждая Т-образная секция имеет индуктивность 1 мкГн в каждой ветви Т, их можно объединить в смежных секциях и использовать индуктор 2 мкГн.
• Выбор компонентов: Выбор компонентов для любого фильтра, и в данном случае для конструкции фильтра нижних частот, важен.Следует использовать компоненты с жесткими допусками, чтобы гарантировать получение требуемых характеристик. Также необходимо проверить температурную стабильность, чтобы убедиться, что компоненты фильтра не изменяются значительно с температурой, тем самым изменяя производительность.
• Расположение фильтра: Необходимо соблюдать осторожность при размещении фильтра. Это следует делать не только для частот полосы пропускания, но, что более важно, для частот в полосе заграждения, которые могут значительно превышать частоту среза фильтра нижних частот.Емкостная и индуктивная связь являются основными элементами, которые ухудшают характеристики фильтра. Соответственно, вход и выход фильтра должны быть разделены. Следует использовать короткие провода и дорожки, компоненты из соседних секций фильтра должны быть разнесены. При необходимости используются экраны, а на входе и выходе используются качественные разъемы и коаксиальный кабель.

Эти уравнения представляют собой очень простой метод разработки трехполюсного фильтра нижних частот.Хотя они могут не обеспечивать точный требуемый отклик, например, Бесселя, Чебышева и т. Д., Они, тем не менее, очень просты в использовании и представляют собой идеальное решение для большинства конструкций фильтров нижних частот. Рисунки или даже сами уравнения также можно преобразовать, чтобы получить конструкцию фильтра верхних частот.

Другие важные темы по радио:
Радиосигналы Типы и методы модуляции Амплитудная модуляция Модуляция частоты OFDM ВЧ микширование Петли фазовой автоподстройки частоты Синтезаторы частот Пассивная интермодуляция ВЧ аттенюаторы RF фильтры RF циркулятор Типы радиоприемников Радио Superhet Избирательность приемника Чувствительность приемника Обработка сильного сигнала приемника Динамический диапазон приемника
Вернуться в меню тем радио.. .

Типы пассивных фильтров нижних частот

Что такое фильтр нижних частот? Пассивный фильтр нижних частот и его типы с примерами.

Пассивный фильтр нижних частот — это тип фильтра нижних частот, который состоит из пассивных электронных компонентов, таких как резистор, конденсатор и катушка индуктивности. Коэффициент усиления пассивного фильтра нижних частот всегда меньше или равен 1. Таким образом, амплитуда его выходного сигнала всегда меньше амплитуды входного сигнала.Однако они просты и легки в разработке. В этой статье мы обсудим пассивный фильтр нижних частот и его типы с примерами.

Фильтр нижних частот

Фильтр нижних частот или LPF — это тип фильтра, который пропускает низкочастотные сигналы и блокирует высокочастотные сигналы. Частоты ниже выбранной частоты, известной как частота среза, пропускаются, тогда как любая частота выше частоты среза блокируется фильтром.

Фильтры нижних частот бывают двух типов:

В этой статье мы обсудим только пассивный фильтр нижних частот, так как активные фильтры нижних частот уже описаны в другом посте. Пассивные фильтры нижних частот классифицируются в соответствии с порядком расположения фильтров. мы обсудим 1 ^st и 2 ^nd фильтр нижних частот.

Фильтр нижних частот первого порядка

Фильтр нижних частот первого порядка — это простейшая форма фильтров нижних частот, состоящая только из одного реактивного компонента i.e Конденсатор или индуктор. Резистор используется с конденсатором или индукторами для формирования RC или RL пассивного фильтра нижних частот соответственно. Ниже приводится краткое описание фильтров нижних частот RC & RL с примерами.

• RC-фильтр нижних частот
• RL-фильтр нижних частот

RC-фильтр нижних частот

Самый простой пассивный фильтр нижних частот состоит из резистора, соединенного последовательно с конденсатором, и выходной сигнал снимается через конденсатор как показано на рисунке ниже.

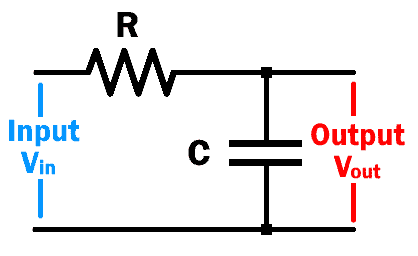
Как мы знаем, конденсатор позволяет передавать высокочастотный сигнал (работать как короткий провод) и блокировать низкочастотный сигнал (работать как открытый провод). Таким образом, когда к цепи применяется низкая частота, конденсатор откроется, и на его клемме появится сигнал, который в конечном итоге будет вытекать как выходной. Однако, когда высокочастотный сигнал достигает конденсатора, происходит короткое замыкание, и выходной сигнал становится нулевым.

Причина, по которой конденсатор блокирует и допускает частоту, заключается в его реактивном сопротивлении, которое определяется как.

X _c = 1 / C = 1 / (2πfC)

Где X _c — реактивное сопротивление конденсатора

f — частота приложенного сигнала

C — это емкость конденсатора

Из приведенного выше уравнения мы можем сказать, что емкостное реактивное сопротивление X _c обратно пропорционально приложенной частоте f . если приложенная частота слишком низкая, реактивное сопротивление X _c будет больше, чем сопротивление резистора, и входной сигнал будет установлен на конденсаторе.Но когда частота f увеличивается, реактивное сопротивление X _c становится ниже, чем сопротивление резистора. Это приводит к низкому падению напряжения (почти незначительному) на конденсаторе по сравнению с резистором.

Частотная характеристика:

Частотная характеристика, также известная как диаграмма Боде схемы, показывает отношение выходного сигнала к входному для указанного диапазона частот. Частотная характеристика фильтра нижних частот приведена ниже:

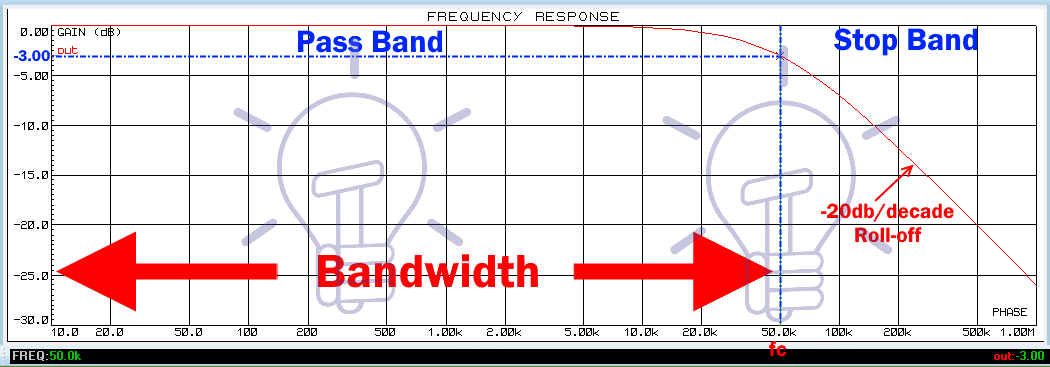
Он содержит некоторые ключевые моменты, такие как частота среза f _c , полоса пропускания , полоса задерживания , полоса пропускания и roll -выкл и др.

Частота среза:

Частота среза, также известная как угловая частота обозначается как f _c — это точка выбранной частоты, в которой мощность выходного сигнала становится -3 дБ или 70,7% входного сигнал. На этой частоте емкостное реактивное сопротивление X _c и сопротивление резистора R становятся равными.

Фильтр нижних частот разрешает частоту ниже частоты среза и блокирует любую частоту выше частоты среза.

Где частота среза рассчитывается по:

R = X _c

R = 1 / (2πfC)

f _c = 1 / (2πRC)

PassBand :

Полоса пропускания — это диапазон частот, который пропускается через фильтр. В фильтре нижних частот частота полосы пропускания ниже, чем частота среза f _c .

StopBand:

Полоса задерживания — это диапазон частот, который блокируется фильтром.В фильтре нижних частот диапазон частот выше частоты среза f _c называется полосой задерживания .

Полоса пропускания:

Полоса пропускания фильтра — это диапазон частот, который проходит без ослабления. Фильтр нижних частот допускает частоту от 0 Гц до f _c Гц . Таким образом, его полоса пропускания составляет f _c -0 = fc Hz .

Спад:

Когда частота увеличивается и достигает частоты среза, усиление фильтра начинает уменьшаться.Скорость уменьшения усиления известна как спад.

Спад фильтра нижних частот порядка 1 ^st составляет -20 дБ на декаду .

Выходное напряжение:

Для расчета выходного напряжения пассивного фильтра нижних частот на любой частоте между резистором и конденсатором применяется правило делителя напряжения. Таким образом, выходное напряжение v _out равно.

V _out = V _in * (X _c / Z)

Где

X _c = емкостное реактивное сопротивление

Z = полное сопротивление цепи

Z = R + jX _c

Z = √ (R ² + X _c ² )

Итак

V _out = V _дюйм * (X _c / √ (R ² + X _c ² ))

Где X _c = 1 / (2πfC)

Усиление:

Коэффициент усиления в соотношении выходного напряжения к входному вольтаж.

Усиление = V _out / V _in

Это усиление обычно описывается как дБ , что является логарифмической формой усиления и определяется как:

Усиление _дБ = 20 log (V _out / V _in )

Обратите внимание на усиление пассивного фильтра нижних частот на приведенном выше графике частотной характеристики. Максимальное усиление остается 0 дБ . В активном фильтре это усиление может быть изменено в соответствии с требованиями.

Пример:

Давайте рассмотрим пример фильтра нижних частот RC с резистором R 1K и конденсатором C 47 нФ .

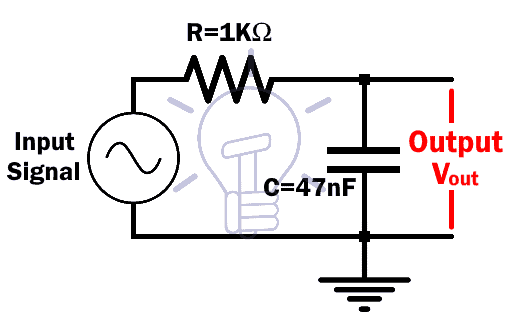
Частота отсечки f _c рассчитывается как:

f _c = 1 / (2πRC)

f _c = 1 / (2π * 10 ³ * 47 * 10 ^-9 )

f _c = 3.38 кГц

Моделирование частотной характеристики с использованием Proteus для данного фильтра нижних частот RC составляет

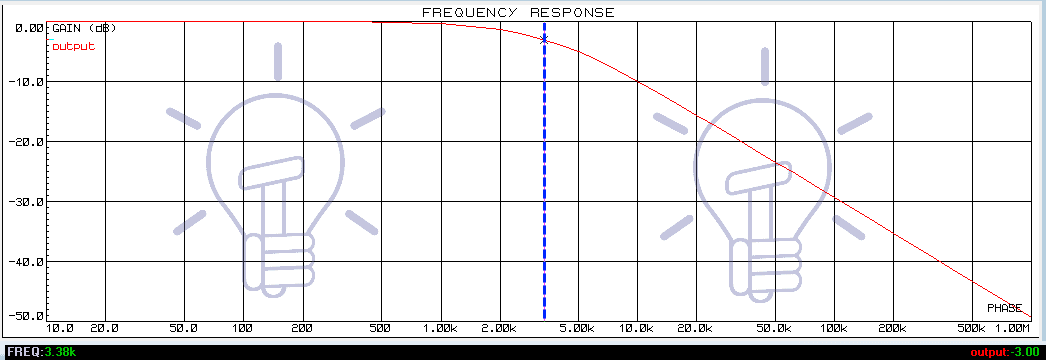
Он ясно показывает усиление -3 дБ при 3,38 кГц , что является частотой среза этого фильтра.

Этот фильтр разрешает любую частоту ниже 3,38 кГц и блокирует любую частоту выше 3,38 кГц . Таким образом, его полоса пропускания составляет 3,38 кГц .

RL Фильтр нижних частот:

Этот тип фильтра нижних частот состоит из последовательно соединенных резистора и индуктора, где выходной сигнал снимается через резистор, как показано на рисунке ниже.

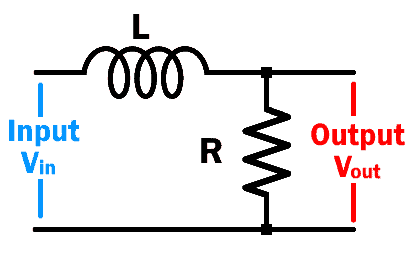
Катушка индуктивности позволяет проходить низкочастотному сигналу, который в конечном итоге устанавливается на резисторе, и блокирует высокочастотный сигнал, который не попадает на нагрузочный резистор.

Индуктор обеспечивает низкое реактивное сопротивление для низкочастотного сигнала и высокое реактивное сопротивление для высокочастотного сигнала. Его реактивное сопротивление определяется выражением:

X _L = L = 2πfL

Согласно приведенному выше уравнению реактивное сопротивление катушки индуктивности прямо пропорционально частоте входного сигнала.

Таким образом, когда частота входного сигнала низкая, его реактивное сопротивление будет ниже, чем сопротивление резистора. Таким образом, результирующее падение напряжения входного сигнала будет максимальным на нагрузочном резисторе.

Когда частота входного сигнала увеличивается, индуктивное сопротивление X _L становится больше, чем сопротивление резистора R . Из-за чего получается незначительное падение напряжения на нагрузочном резисторе. таким образом, входной сигнал блокируется.

Частотная характеристика:

Частотная характеристика RL-фильтра нижних частот аналогична RC-фильтру нижних частот.

Частота среза фильтра нижних частот RL определяется как:

При частоте среза реактивное сопротивление равно сопротивлению

X _L = R

2πfl = R

f _c = R / (2πL)

Где

L = индуктивность катушки индуктивности

R = сопротивление резистора

Выходное напряжение:

Выходное напряжение на любой частоте может быть рассчитано по напряжению разделитель.

V _out = V _in * R / Z

Где Z = полное полное сопротивление цепи.

Z = R + JX _L

Z = √ (R ² + X _L ² )

Итак

V _out = V _{дюйм *} R / √ (R ² + X _L ² )

Где X _L = 2πfL

Пример:

В этом примере мы возьмем резистор 1K и 3mH катушка индуктивности.

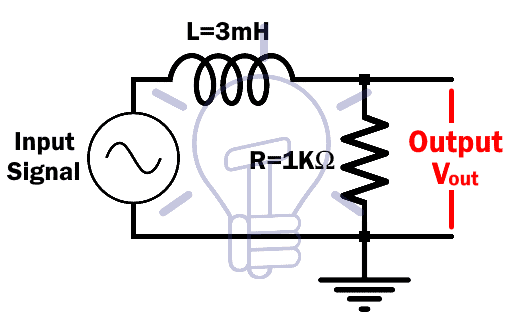
Рассчитаем частоту среза для этой схемы.

f _c = R / (2πL)

f _c = 10 ³ / (2π * 3 * 10 ^-3 )

f _c = 53 кГц

Смоделируем эту схему с помощью Proteus. Частотная характеристика с использованием Proteus приведена ниже:

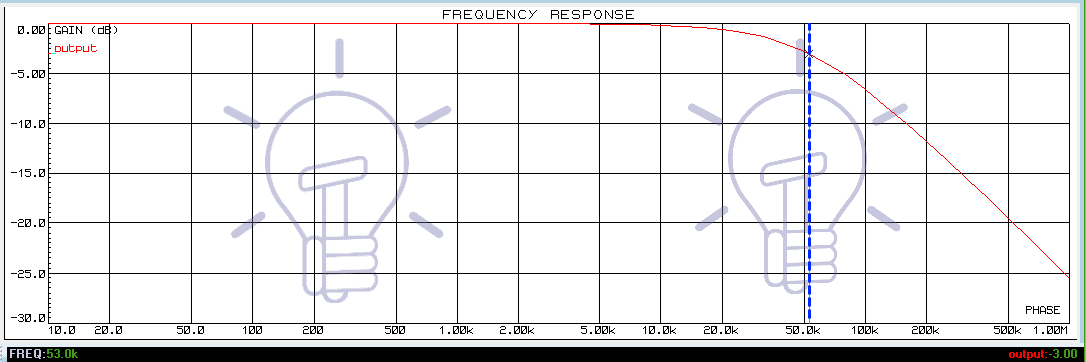
Он четко показывает точку -3 дБ (частота среза), где частота равна 52.9 кГц , что почти равно 53 кГц .

Пассивный фильтр нижних частот второго порядка

Фильтр нижних частот второго порядка состоит из двух каскадных фильтров нижних частот первого порядка. Фильтр нижних частот первого порядка может быть схемой RC или RL . Мы обсудим оба с примерами.

RC-фильтр низких частот

Два RC-фильтра порядка 1 ^st соединены каскадом, образуя фильтр низких частот 2 ^и .Схема RC-фильтра нижних частот порядка 2 ^nd приведена ниже;

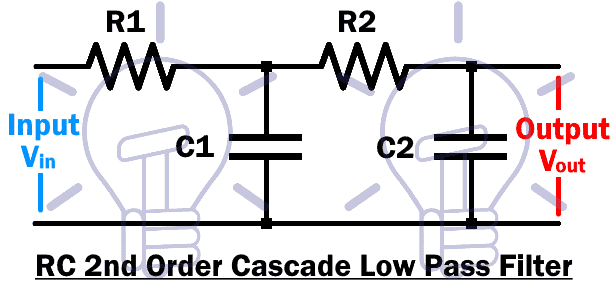
Ступень фильтра нижних частот первого порядка состоит из R ₁ C ₁ , а вторая ступень — из R ₂ C _{2 .}

Выход может быть получен с любого из двух этапов. Первый каскад будет обеспечивать выходной сигнал фильтра нижних частот порядка 1 ^st со спадом -20 дБ / декада .Второй каскад будет обеспечивать выходной сигнал фильтра нижних частот порядка 2 ^и с более крутым спадом -40 дБ / декада . Его частотная характеристика показана ниже.

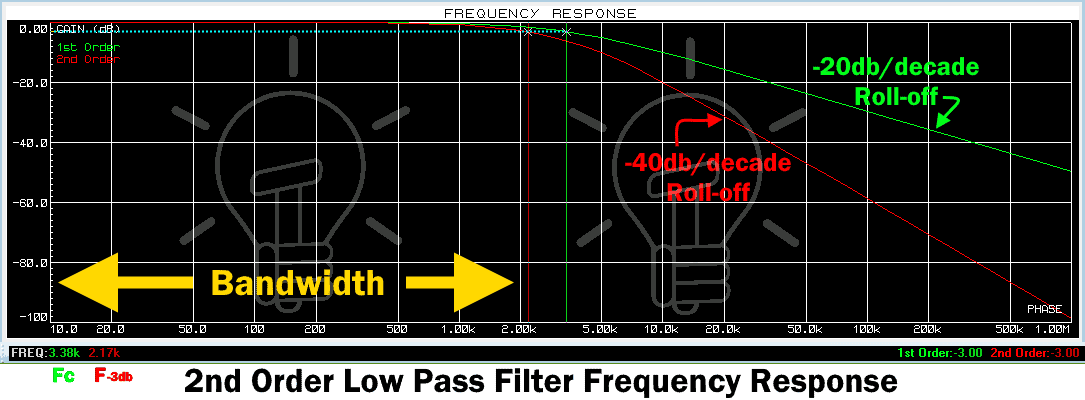
Зеленый сигнал показывает частотную характеристику фильтра нижних частот 1 ^st со спадом -20 дБ / декада . Красный сигнал показывает частотную характеристику фильтра нижних частот 2 ^и со спадом -40 дБ / декада .

Частота среза:

Частота среза или частота среза f _c из 2 ^nd Фильтр нижних частот порядка определяется как

f _c = 1 / {2π√ (R ₁ R ₂ C ₁ C ₂ )}

Если резистор R = R ₁ = R ₂ & конденсатор C = C ₁ = C ₂ , затем

f _c = 1 / (2πRC)

Усиление на угловой частоте:

Коэффициент усиления обычного n фильтра нижних частот порядка на угловой частоте определяется как:

Усиление = (1 / √2) ⁿ

Таким образом, усиление 2 ^nd фильтр нижних частот на угловой частоте f _c составляет

Усиление = (1 / √2) ² = 0.5

Коэффициент усиления дБ будет:

Коэффициент усиления _(дБ) = 20 log (0,5) = -6 дБ

Таким образом, коэффициент усиления 2 ^nd ФНЧ на частоте среза равен -6 дБ .

-3 дБ Частота:

Расчетная частота излома f _c обеспечивает усиление -6 дБ , тогда как частота полосы пропускания фильтра находится на уровне — 3 дБ усиление, которое рассчитывается как:

f _(-3db) = f _c √ (2 ^{(1 / n)} -1)

Где n — порядок фильтра, а f _c — вычисленная угловая частота. f _(-3db) уменьшаются с увеличением порядка фильтра. Это означает, что порядок увеличения фильтра обеспечивает более крутой или быстрый спад.

Пример

В этом примере мы взяли резистор R ₁ = 1 кОм , R ₂ = 10 кОм и конденсатор C ₁ = 47 нФ , C ₂ = 4,7 нФ

Примечание: тот факт, что мы используем R ₂ > 10R ₁ & C ₂ <10C ₁ , вызван эффектом нагрузки, иначе выходной сигнал будет содержать ошибки.Чтобы уменьшить влияние нагрузки, сопротивление второй ступени должно быть намного больше, чем первой ступени.

Частота отсечки этой цепи будет

f _c = 1 / {2π√ (R ₁ R ₂ C ₁ C ₂ )}

f _c = 1 / {2π√ (10 ³ * 10 * 10 ³ * 47 * 10 ^-9 * 4,7 * 10 ^-9 )}

f _c = 3,38 кГц

Эта частота находится на уровне -6 дБ при усилении .Теперь вычислим f _(-3db)

f _(-3db) = fc √ (2 ^(1/2) -1)

f _(-3db) = 3,38 * 10 ³ √ (2 ^(1/2) -1)

f _{(-3 дБ)} = 2,17 кГц

Таким образом, этот фильтр нижних частот допускает частоту менее 2,17 кГц , таким образом, его полоса пропускания составляет 2,17 кГц .

Давайте смоделируем этот пример с помощью Proteus .Ниже приведена частотная характеристика указанного примера.

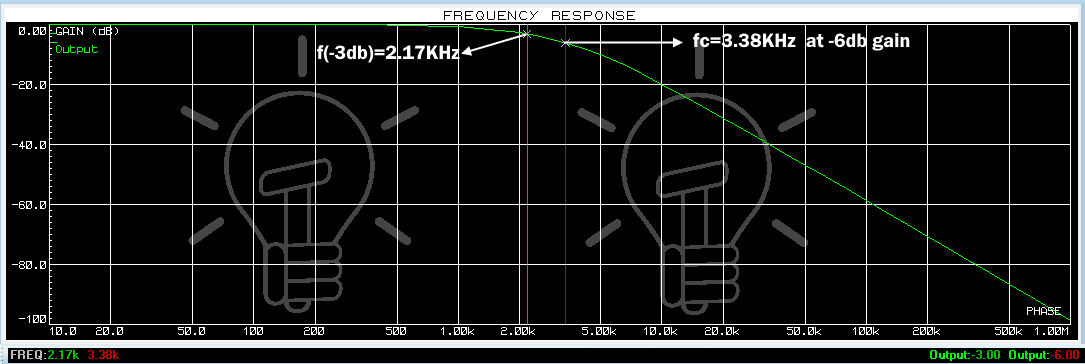
Этот график ясно показывает частоту -3 дБ при 2,17 кГц , которую мы рассчитали ранее.

RL Фильтр нижних частот:

Два каскада фильтра нижних частот RL каскадно соединены вместе, образуя фильтр нижних частот 2 ^и . Первая ступень состоит из L ₁ R ₁ , а вторая ступень состоит из L ₂ R ₂ .Его схема приведена ниже.

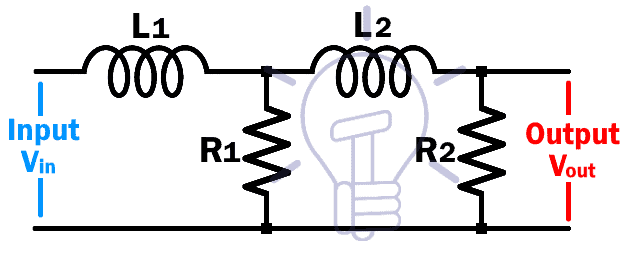
Ступень 1 ^st представляет собой фильтр нижних частот 1 ^st , выходной сигнал которого обеспечивает спад -20 дБ / декада . Каскад 2 ^и обеспечивает фильтр нижних частот порядка 2 ^и со спадом спада -40 дБ / декада .

Угловая частота

Угловая частота или частота среза f _c из 2 ^nd Фильтр нижних частот порядка определяется как.

f _c = {√ (R ₁ R ₂ )} / {2π√ (L ₁ L ₂ )}

Если резистор R = R ₁ = R ₂ и индуктор L = L ₁ = L ₂ , затем

f _c = R / (2πL)

Коэффициент усиления на угловой частоте:

Коэффициент усиления на частота излома определяется по формуле:

Усиление = (1 / √2) ⁿ

Где n — порядок фильтра.Таким образом, усиление 2 ^nd фильтр нижних частот порядка:

Усиление = (1 / √2) ² = 0,5

Усиление дБ составляет

Усиление _(дБ) = 20 log (0,5) = -6 дБ

-3 дБ Частота

Фактическая частота среза фильтра находится на уровне –3 дБ при усилении . Для расчета частоты -3 дБ мы будем использовать:

f _{(-3 дБ)} = f _c √ (2 ^{(1 / n)} -1)

Где n — это порядок фильтр.

Пример:

Возьмем резистор R ₁ = 1K , R ₂ = 10K и индуктор L ₁ = 3 мГн , L ₂ = 30 мГн .

Мы взяли R ₂ > 10R ₁ и L ₂ > 10 L ₁ из-за эффекта нагрузки, описанного ранее. Импеданс следующей ступени должен быть как минимум в 10 раз выше, чем на предыдущей ступени.

Частота среза этого фильтра составляет

f _c = {√ (R ₁ R ₂ )} / {2π√ (L ₁ L ₂ )}

f _c = {√ (10 ³ * 10 * 10 ³ )} / {2π√ (3 * 10 ^-3 * 30 * 10 ^-3 )}

f _c = 53 кГц

Частота находится на уровне -6 дБ , поэтому мы рассчитаем частоту -3 дБ , которая определяется по формуле:

f _{(-3 дБ)} = f _c √ (2 ^{(1 / 2)} -1)

f _(-3dB) = 53 * 10 ³ √ (2 ^(1/2) -1)

f _(-3dB) = 34.11 кГц

Это частота -3 дБ этого фильтра. Моделирование этого фильтра Proteus приведено ниже.

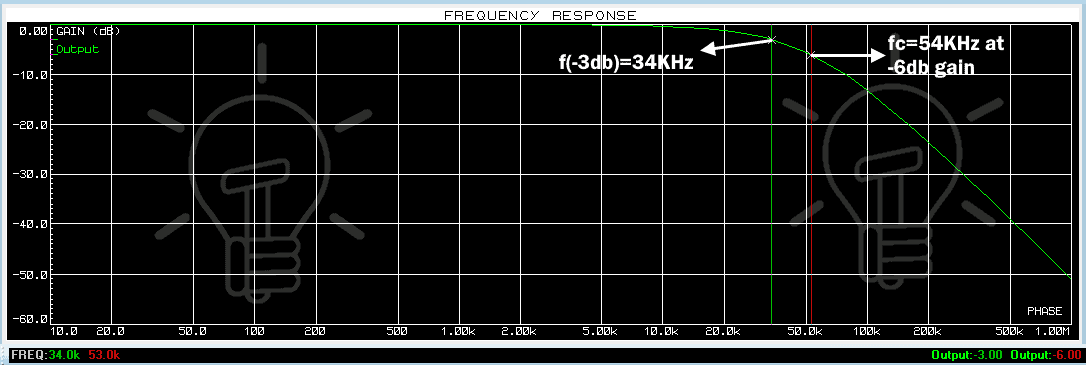
На графике показано усиление -3 дБ при частоте 34,11 кГц . и вы можете четко видеть разницу между спадом фильтров нижних частот порядка 1 ^st и 2 ^и .

Ограничения пассивного фильтра нижних частот:

• В пассивном фильтре нижних частот нет усиления входного сигнала.
• Его коэффициент усиления остается меньше или равным 1.
• Каскадные каскады для пассивных фильтров более высокого порядка приводят к потере амплитуды сигнала.
• Импеданс нагрузки влияет на характеристики фильтра.

Связанное сообщение: Резисторы и типы резисторов | Фиксированные, переменные, линейные и нелинейные

Что необходимо знать инженеру-электронику о пассивных фильтрах нижних частот — Блог о пассивных компонентах

• Дом
• Политика конфиденциальности
• Реклама и членство в EPCI
• Около

Нет результата

Просмотреть все результаты

НОВОСТНАЯ РАССЫЛКА

• Дом
• Новости по категориям
  • Все
  • Аэрокосмическая промышленность и оборона
  • Приложения
  • Автомобильная промышленность
  • Конденсаторы
  • Фильтры
  • Предохранители
  • Индукторы
  • Промышленные
  • Интегрированные пассивные компоненты
  • Рынок и цепочка поставок
  • Медицина
  • Новые материалы и поставки
  • 50 Новые технологии Нелинейные пассивные элементы
  • Резисторы
  • ВЧ и СВЧ
  • Телекоммуникации
  

  APITech объявляет о выпуске высоковольтных керамических конденсаторов

  

  PREMO представляет семейство компактных никель-цинковых трансформаторов с низкими потерями для связи по линиям электропередач.

  

  NCI стабилизирует поставку керамических конденсаторов с помощью высококачественного титаната бария

  

  YAGEO продвигает 5G за счет расширения производства чип-резисторов

  

  KEMET продвигает полимерные решения автомобильного класса для авионики и автомобильной промышленности

  Решение проблем проектирования конденсаторов для подавления электромагнитных помех

  

  TDK представляет новые компактные алюминиевые электролитические конденсаторы Snap-In с высоким напряжением CV и высоким током пульсаций

  

  Мемристоры на основе графена перспективны для вычислений на основе мозга

  

  LTspice Анализ схем наихудшего случая с неидеальными резисторами при минимальных прогонах моделирования

  Трендовые теги

  • Ток пульсации
  • RF
  • Ток утечки
  • Тантал против керамики
  • Демпфер
  • Низкое ESR
  • Проходной канал
  • Снижение номинальных значений
  • Диэлектрическая постоянная
  • Новые продукты
  • Отчеты о рынке
• Видеоканал с возможностью фильтрации
  • Все
  • Видео с конденсаторами
  • Видео с фильтрами
  • Видео с предохранителями
  • Видео с индуктора
  • Видео с нелинейными пассивными элементами
  • Видео с резисторами
  

  Kemet Webinar Automotive Series: Почему системы 48 В идеальны для автомобилей будущего

  

  Kemet Webinar Automotive Series: Разработка эффективных и надежных бортовых зарядных устройств

  

  Интервью Мураты о большом взрыве 5G и его влиянии на рынок

  

  Защита переменного тока и управление двигателем в системах отопления, вентиляции и кондиционирования воздуха — Вебинар Littelfuse и Mouser Electronics

  

  Веб-семинар Würth Elektronik: Простота создания микромодулей — Советы и хитрости

  

  Операционные усилители в качестве активных полосовых и активных полосовых фильтров

  

  Вебинар по пассивным компонентам Kemet Серия автомобилей: Электрификация силовых агрегатов в транспортных средствах

  

  Вебинар Vishay: высокомощные, высокотемпературные компоненты для автомобильных силовых агрегатов 48 В

  

  Вебинар Kemet, серия «Автомобильная промышленность: технологии, способствующие инновациям в автономных транспортных средствах»

  Трендовые теги

  • Описание конденсаторов
  • Описание индукторов
  • Описание резисторов
  • Объяснение фильтров
  • Видеоинструкции по применению
  • EMC
  • Новые продукты
  • Пульсации тока
  • Моделирование
  • Тантал против керамики
• Кто есть Whoin Passives
• События
• Обзоры рынка

• Дом
• Новости по категориям
  • Все
  • Аэрокосмическая промышленность и оборона
  • Приложения
  • Автомобильная промышленность
  • Конденсаторы
  • Фильтры
  • Предохранители
  • Индукторы
  • Промышленные
  • Интегрированные пассивные компоненты
  • Рынок и цепочка поставок
  • Медицина
  • Новые материалы и поставки
  • 50 Новые технологии Нелинейные пассивные элементы
  • Резисторы
  • ВЧ и СВЧ
  • Телекоммуникации
  

  APITech объявляет о выпуске высоковольтных керамических конденсаторов

  

  PREMO представляет семейство компактных никель-цинковых трансформаторов с низкими потерями для связи по линиям электропередач.

  

  NCI стабилизирует поставку керамических конденсаторов с помощью высококачественного титаната бария

  

  YAGEO продвигает 5G за счет расширения производства чип-резисторов

  

  KEMET продвигает полимерные решения автомобильного класса для авионики и автомобильной промышленности

  Решение проблем проектирования конденсаторов для подавления электромагнитных помех

  

  TDK представляет новые компактные алюминиевые электролитические конденсаторы Snap-In с высоким напряжением CV и высоким током пульсаций

  

  Мемристоры на основе графена перспективны для вычислений на основе мозга

  

  LTspice Анализ схем наихудшего случая с неидеальными резисторами при минимальных прогонах моделирования

  Трендовые теги

  • Ток пульсации
  • RF
  • Ток утечки
  • Тантал против керамики
  • Демпфер
  • Низкое ESR
  • Проходной канал
  • Снижение номинальных значений
  • Диэлектрическая постоянная
  • Новые продукты
  • Отчеты о рынке
• Видеоканал с возможностью фильтрации
  • Все
  • Видео с конденсаторами
  • Видео с фильтрами
  • Видео с предохранителями
  • Видео с индуктора
  • Видео с нелинейными пассивными элементами
  • Видео с резисторами
  

  Kemet Webinar Automotive Series: Почему системы 48 В идеальны для автомобилей будущего

  

  Kemet Webinar Automotive Series: Разработка эффективных и надежных бортовых зарядных устройств

  

  Интервью Мураты о большом взрыве 5G и его влиянии на рынок

  

  Защита переменного тока и управление двигателем в системах отопления, вентиляции и кондиционирования воздуха — Вебинар Littelfuse и Mouser Electronics

  

  Веб-семинар Würth Elektronik: Простота создания микромодулей — Советы и хитрости

  

  Операционные усилители в качестве активных полосовых и активных полосовых фильтров

  

  Вебинар по пассивным компонентам Kemet Серия автомобилей: Электрификация силовых агрегатов в транспортных средствах

  

  Вебинар Vishay: высокомощные, высокотемпературные компоненты для автомобильных силовых агрегатов 48 В

  

  Вебинар Kemet, серия «Автомобильная промышленность: технологии, способствующие инновациям в автономных транспортных средствах»

  Трендовые теги

  • Объяснение конденсаторов
  • Объяснение индукторов
  • Объяснение резисторов
  • Объяснение фильтров

Как работают фильтры — Анимации.

• Изучив этот раздел, вы сможете описать:
• Как пассивные фильтры достигают частотно-избирательного затухания и изменения фазы со ссылкой на векторные диаграммы.
• • Фильтры высоких частот.
• • Фильтры нижних частот.

CR Работа фильтра.

На рисунках 8.2.1 и 8.2.2 показаны два распространенных метода использования C и R вместе для изменения сигналов переменного тока. Эти комбинации CR используются для многих целей в самых разных схемах. В этом разделе описываются их эффекты при использовании в качестве фильтров с синусоидальными сигналами различной частоты, такими как простой тон или регуляторы низких / высоких частот в звуковых кругах. Подобные комбинации CR также используются для изменения формы несинусоидальных волн. Такие волны, как прямоугольные волны, содержат множество гармоник с разными частотами, и за счет уменьшения амплитуды некоторых из этих гармоник форма волны изменяется.Методы, используемые для этой цели, описаны в разделах «Дифференциаторы и интеграторы» далее в этом модуле.

CR фильтр верхних частот

Рис. 8.2.1 CR фильтр верхних частот

Схема CR, показанная на рис. 8.2.1, при использовании с синусоидальными сигналами называется ФИЛЬТРОМ HIGH PASS. Его цель состоит в том, чтобы позволить высокочастотным синусоидальным волнам беспрепятственно проходить от его входа к его выходу, но уменьшать амплитуду (ослаблять) низкочастотные сигналы. Типичным применением этой схемы является коррекция частотной характеристики (коррекция тона) в аудиоусилителе.

Как описано в Модуле 6, сопротивление постоянно на любой частоте, но сопротивление току, обеспечиваемое конденсатором (C), однако, происходит из-за емкостного реактивного сопротивления X _C , которое больше на низких частотах, чем на высоких частотах.

Реактивное сопротивление конденсатора (X _C ) и сопротивление резистора (R) на рис. 8.2.1 действуют как делитель потенциала, размещенный поперек входа, а выходной сигнал берется из центра двух компонентов.На низких частотах, где X _C намного больше, чем R, доля напряжения сигнала на R будет меньше, чем на C, и поэтому выходной сигнал будет ослаблен. На более высоких частотах с помощью подходящего выбора значений компонентов достигается то, что сопротивление R будет намного больше, чем (теперь низкое) реактивное сопротивление X _C , поэтому большая часть сигнала формируется через R, а небольшая или затухания не произойдет.

CR фильтр низких частот

Рис 8.2.2 Фильтр низких частот CR

На Рис. 8.2.2 положение резистора и конденсатора поменялось местами, так что на низких частотах высокое реактивное сопротивление, обеспечиваемое конденсатором, позволяет всему или почти всему входному сигналу развиваться как выходное напряжение на X _C . . Однако на более высоких частотах X _C становится намного меньше, чем R, и теперь на X _C передается небольшая часть входного сигнала. Таким образом, схема ослабляет высокие частоты, подаваемые на вход, и действует как фильтр низких частот.

Полоса частот, ослабленная фильтрами высоких и низких частот, зависит от значений компонентов. Частота, на которой начинается или заканчивается затухание, может быть выбрана подходящим выбором компонентов. В случаях коррекции звукового тона резистор можно сделать регулируемым, что позволяет срезать переменное количество низких или высоких частот (низких или высоких частот). Это основа большинства недорогих регуляторов тембра

.

Фильтры верхних и нижних частот также могут быть построены из L и R. В этом случае действие такое же, как и для схемы CR, за исключением того, что действие X _L является обратным по отношению к X _C .Поэтому в фильтрах LR положение компонентов меняется на обратное.

Изменение фазы в фильтрах

Приведенное выше описание фильтров верхних и нижних частот объясняет, как они работают с точки зрения сопротивления и реактивного сопротивления. Он показывает, как коэффициент усиления (Vout / Vin) отличается на высоких и низких частотах из-за относительных значений X _C и R. Однако это простое объяснение не принимает во внимание фазовые отношения между конденсаторами или катушками индуктивности и резисторами. Чтобы точно рассчитать значения напряжения на компонентах фильтра, необходимо учитывать фазовые углы, а также сопротивление и реактивное сопротивление.Это можно сделать с помощью векторных диаграмм для вычисления значений графически или с помощью раздела алгебры, используя «комплексные числа» и «j-нотацию». Однако эти расчеты также могут быть выполнены с использованием немного большего, чем расчеты реактивного сопротивления, полученные в модуле 6, и расчеты треугольника импеданса из модуля 7.

Проблема:

Вычислите размах напряжений V _r , появляющихся на R и V _c , появляющихся на C, когда напряжение питания переменного тока 2 В (пиковый) на частоте 1 кГц подается на схему, как показано.

Хотя C и R образуют делитель потенциала на V _s , эти значения невозможно вычислить с помощью уравнения делителя потенциала (поскольку необходимо также учитывать фазовые углы):

Выполните следующие действия:

1. Найдите значение емкостного реактивного сопротивления X _C , используя:

2. Используйте треугольник импеданса, чтобы найти Z (полное сопротивление всей цепи).

3.Зная, что напряжение питания V _s возникает через Z, следующим шагом будет вычисление вольт на Ом (В / Ом),

Поскольку вольт на Ом будет одинаковым для каждого компонента, как и для полного сопротивления цепи, результат шага 3 теперь можно использовать для определения напряжений на C и R.

При необходимости фазовый угол θ можно также определить с помощью тригонометрии, как описано в разделе «Вычисления фазоров», модуль 5.4 (метод 3). Чтобы найти угол θ (разность фаз между напряжением питания V _S и током питания, который должен быть в той же фазе, что и V _R ), можно использовать два уже найденных напряжения.

Поскольку цепи, содержащие в дополнение к сопротивлению емкость (или индуктивность), влияют на фазовые соотношения синусоидальных сигналов. Это позволяет использовать те же самые схемы для изменения ФАЗЫ сигналов вместо или для изменения амплитуды.

CR Работа фильтра

Рис 8.2.3 демонстрирует, как векторные диаграммы могут объяснить как амплитудные, так и фазовые эффекты CR-фильтров. Щелкните стрелки направления, чтобы увидеть, как фильтр верхних частот работает на разных частотах, и обратите внимание, что это входное напряжение (V _IN , очевидно, изменяет фазу, но это просто потому, что вектор тока цепи (и, следовательно, V _R , который всегда находится в фазе с током) используется как статический эталонный вектор. Следует помнить, что между V _IN и V _OUT происходит изменение фазы от 0 ° до 90 °, которая зависит от частоты сигнала.

Использование векторных диаграмм для объяснения фильтра высоких частот показывает, что:

• В фильтре верхних частот (рис. 8.2.3) на низких частотах выходной сигнал V _OUT (V _R ) намного меньше, чем V _IN (V _C ), а фазовый сдвиг до 90 ° происходит, когда выходная фаза опережает входную.

• На высоких частотах разница между относительными амплитудами V _OUT (V _R ) и V _IN незначительна или отсутствует, и сдвиг фазы небольшой или отсутствует.На угловой частоте f _c фазовый сдвиг составляет 45 ° и ниже этого графика график Боде показывает, что усиление частоты падает с постоянной скоростью -20 дБ за декаду.

Для получения дополнительной информации о графиках Боде и о том, как их можно использовать вместе с векторными диаграммами для иллюстрации работы фильтра нижних частот, см. Графики Боде, где на рис. 8.3.2 аналогично показано действие фильтра нижних частот CR. В этой схеме обратите внимание, что V _OUT = V _C , поэтому выходная фаза отстает от входной фазы примерно на -90 °, в зависимости от входной частоты

Рис.8.2.3 Работа фильтра высоких частот.

Фильтры нижних частот — все RF

1986 Фильтры нижних частот от 47 производителей, перечисленные во всем, RF

RF Фильтры низких частот от ведущих производителей перечислены ниже. Используйте фильтры, чтобы сузить список продуктов в соответствии с вашими требованиями. Загрузите таблицы данных, сравните продукты и запросите расценки. Ваш запрос будет направлен производителю и его дистрибьюторам, которые ответят вам с предложением.

Бета

Описание: DC до 1207.Миниатюрный SMD фильтр нижних частот, 5 МГц

Описание: 12-секционная серия фильтров нижних частот, выбор Fco от 3,5 до 6 ГГц

Тип:

Фильтр сосредоточенных компонентов, фильтр Чебышева

Частота:

от постоянного тока до 3,5 / 6 ГГц

Частота полосы задерживания:

Chosen Fco x от 1,095 до 18 ГГц

Вносимая потеря:

1-2 дБ

Тип упаковки:

Модуль с коннектором

Оценка:

Коммерческий, Космический, Военный

больше информации Просмотреть продукты этой компании

Описание: от 1000 до 2000 МГц, SMA — женский фильтр нижних частот

Тип:

Фильтр сосредоточенных компонентов

Конфигурация:

Фильтр низких частот

Частота:

от 1000 до 2000 МГц

Отклонение:

20 мин.@ 2400 МГц

Тип упаковки:

Модуль с коннектором

больше информации Просмотреть продукты этой компании

Описание: Фильтр нижних частот от 0 до 1600 МГц в прочном корпусе

Вносимая потеря:

Менее 0,4 дБ

Тип упаковки:

Крепление на поверхность

Оценка:

Военный, Космический, Коммерческий

больше информации Просмотреть продукты этой компании

Параметры фильтра нижних частот RF

Фильтр нижних частот (LPF) пропускает низкочастотные сигналы и блокирует сигналы выше определенной частоты.Точка, до которой он передает сигналы, называется частотой среза.
При выборе ВЧ фильтра нижних частот учитывайте следующие характеристики:

• Частота среза: Это частота, ниже которой сигнал проходит с минимальными потерями. Любой сигнал выше этой частоты ослабляется.
• Полоса пропускания или полоса пропускания : Это частота ниже частоты среза.
• Stopband: это частота выше частоты среза.
• Вносимая потеря: Это потеря сигнала в полосе пропускания фильтра. Обычно он очень низкий и выражается в дБ.
• Затухание / Подавление: Затухание дает измерение того, насколько хорошо фильтр может подавлять нежелательные частотные составляющие. Это потеря сигнала выше частоты среза. Он представлен в дБ. Всегда предпочтительнее более высокое затухание.
• Уровень мощности: Это максимальная входная мощность, с которой может справиться фильтр.

все, что есть в РФ низкочастотные фильтры ведущих производителей. Сузьте список параметров, выбрав полосу пропускания, уровень затухания, вносимые потери, уровень мощности и другой стиль упаковки. Как только вы найдете RF-фильтр нижних частот, который соответствует вашим требованиям, вы сможете просматривать спецификации продукта, загружать таблицы данных и запрашивать расценки. Ваш запрос будет отправлен компаниям или их дистрибьюторам в вашем регионе, которые свяжутся с вами с необходимой информацией.

.

No related posts.