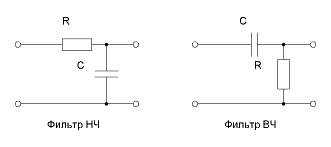
Расчет фильтров нижних и верхних частот
Практический расчет фильтров верхних и нижних частот (RC и LC фильтров)
Доброго дня уважаемые радиолюбители!
Сегодня, на сайте “Радиолюбитель”, на очередном занятии “Практикума начинающего радиолюбителя”, мы с вами рассмотрим порядок расчета фильтров верхних и нижних частот.
Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).
В первую очередь определимся, что понятия “верхние” и “нижние” частоты относятся к звукотехнике, а понятия “высокие” и “низкие” частоты – относятся к радиотехнике.
Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (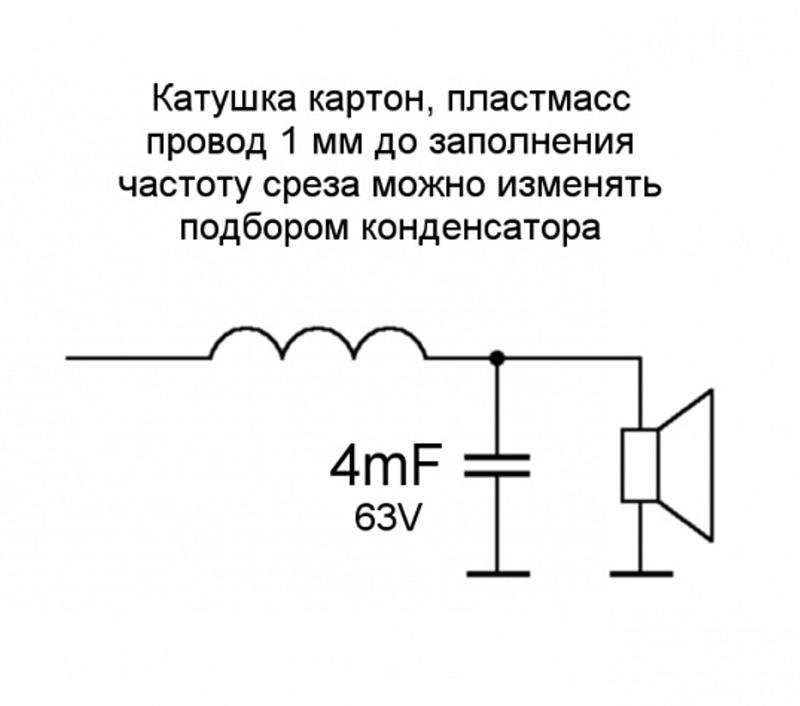 Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный.
Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный.
Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ).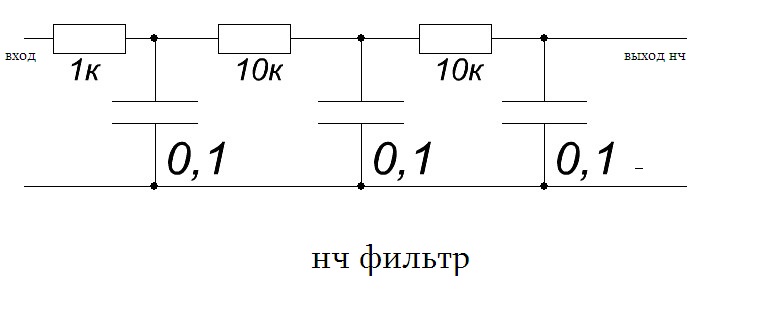 Что это за показатель.
Что это за показатель.
АЧХ фильтра показывает как изменяется уровень амплитуду сигнала проходящего через этот фильтр в зависимости от частоты сигнала.
Тут же появляется еще одно определение: частота среза.
Частота среза – это частота, на которой происходит спад амплитуды выходного сигнала до значения равного 0,7 от входного.
Например, если при частоте входного сигнала 1 кГц амплитудой 1 вольт на выходе фильтра амплитуда входного сигнала уменьшается до 0,7 вольта, то частота 1 кГц является частотой среза данного фильтра.
И последнее определение –
Крутизна частотной характеристики фильтра – это показатель того, на сколько резко изменяется амплитуда входного сигнала на выходе при изменении его частоты. Чем быстрее происходит спад АЧХ тем лучше.
Чем быстрее происходит спад АЧХ тем лучше.
Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах.
Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала. Такое сопротивление называется
Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:
Xc=1/2пFС где:
Хс – реактивное сопротивление конденсатора;
п – оно и в Африке “пи”;
F – частота;
С – емкость конденсатора.
То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.
А реактивное сопротивление катушки индуктивности вот этой формулой:
XL=2пFL где:
XL – реактивное сопротивление катушки индуктивности;
п – оно и в России “пи”;
F – частота сигнала;
L – индуктивность катушки
Частотные фильтры бывают нескольких типов:
– одноэлементные;
– Г- образные;
–
– П – образные;
– многозвенные.
В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов (фильтры с катушками индуктивности трогать не будем).
Одноэлементный фильтр
— фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот).
Г – образный фильтр
Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:
С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.
Формулы для расчета параметров делителя напряжения:
Uвх=Uвых*(R1+R2)/R2
Uвых=Uвх*R2/(R1+R2)
Rобщ=R1+R2
R1=Uвх*R2/Uвых – R2
R2=Uвых*Rобщ/Uвх
К примеру, нам дано:
Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 В
Порядок расчета:
2. Определяем R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм
3. Проверяем Uвых=10*7000/(3000+7000)= 7 В
Что нам и требовалось.
Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже.
ВАЖНО!
Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз.
Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор.
Как вы уже знаете, конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально.
При замене сопротивления R1 на конденсатор (при этом на высоких частотах ток через него проходит беспрепятственно, а на низких ток через него не проходит) мы получим фильтр верхних частот.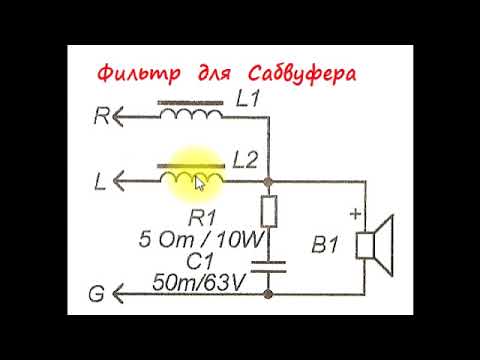
А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот.
Как я уже сказал, уважаемые радиолюбители, мы не будем глубоко нырять в дебри электротехники, иначе мы заблудимся и забудем о чем шла речь. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему.
Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей.
Порядок расчета Г-образного фильтра верхней частоты
В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен.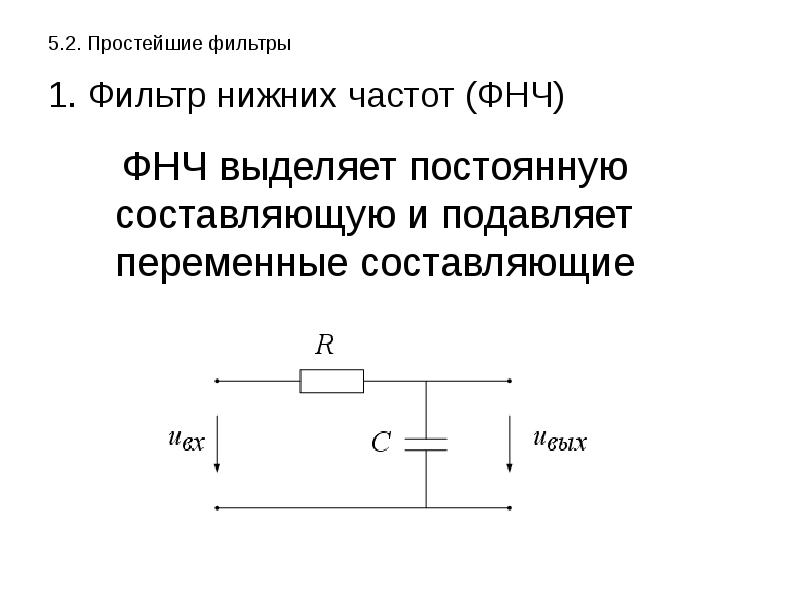 А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.
А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.
Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 —> C=1/2пFR1:
C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.
Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.
Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.
? Для справки:
? 1 мкФ = 10-6 Ф = 0,000 001 Ф
? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф
? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф
и так далее…
Порядок расчета Г-образного фильтра нижней частоты
Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.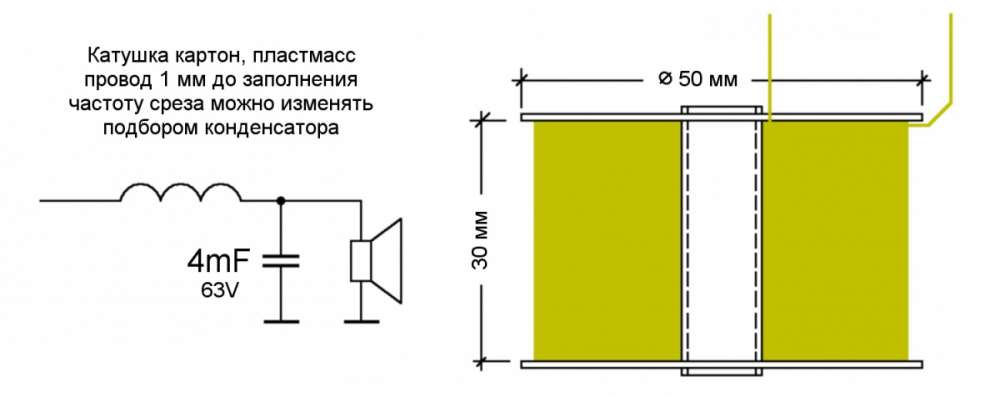
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 —> C=1/2пFR2:
C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.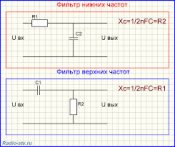
Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.
Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.
Т – образный фильтр
Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра.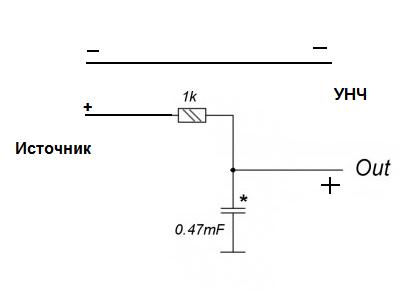 Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:
Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:
П – образный фильтр
П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных.
Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.
Для написания статьи, кроме всего прочего использовались материалы с сайта www.meanders.ru, автором и владельцем которого является Александр Мельник, за что ему большое и бесконечное (меандровское) спасибо.
Простой активный фильтр для двухполосного усилителя
В статье речь пойдет об активном фильтре для двухполосного усилителя. Фильтр не нуждается в трудоемкой настройке и выполнен на доступных ОУ.Первый раз эту схему я собирал лет 10 назад, нужно было раскачать колонки Радиотехника S90 не очень мощным самодельным усилителем (Ватт 25-30 навскидку), цель — узнать на что вообще способны эти колонки.
Но мощности усилителя явно не хватало.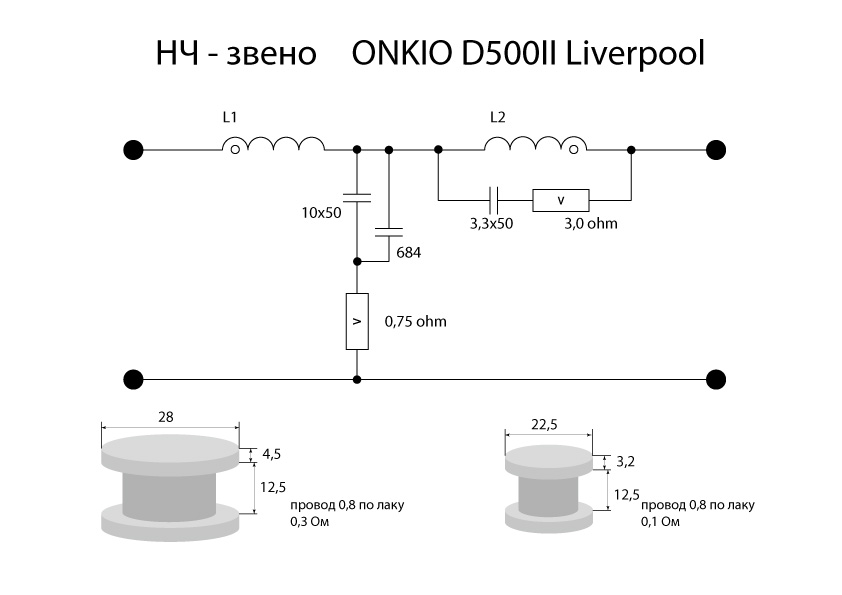 И в одной интересной книжке я набрел на схему этого фильтра. Решил попробовать раскачать S90 двухполосным усилителем.
И в одной интересной книжке я набрел на схему этого фильтра. Решил попробовать раскачать S90 двухполосным усилителем.
Одно из преимуществ заключается в том, что при перегрузке низкочастотного канала, его искажения хорошо маскируются СЧ-ВЧ звеном, следовательно максимальная неискаженная мощность на слух становится заметно больше.
В итоге мне удалось раскачать одну колонку так, что шифер на гараже стал трещать.
Содержание / Contents
Входной сигнал подан на неинвертирующий вход операционного усилителя МС1, который выполняет функции активного фильтра низких частот с крутизной спада частотной характеристики 18 дБ/октаву, и на неинвертирующий вход операционного усилителя МС2, который выполняет функции дифференциального усилителя с коэффициентом передачи по напряжению Ku=1.
На инвертирующий вход МС2 подан сигнал с выхода фильтра низких частот МС1. В дифференциальном усилителе МС2 из спектра входного сигнала вычитается его низкочастотная часть, и на выходе МС2 появляется только высокочастотная часть входного сигнала.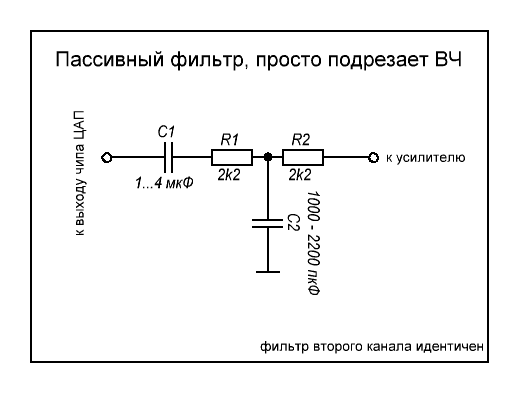
Таким образом, требуется лишь обеспечить заданную частоту среза фильтра низких частот, которая и будет частотой разделения. Значения элементов фильтра находятся из соотношений C1 = C2 = C3; R1=R4; R5=R1/6,8; R1C1=0,4/Fp, где Fр — частота разделения.
R1 я брал 22 кОм, а дальше все рассчитывается по формулам в зависимости от требуемой частоты разделения.
В качестве операционных усилителей пробовал К157УД2 (сдвоенный ОУ — 2 корпуса) и К1401УД2 (счетверенный ОУ — печатка под него), оба показали хорошие результаты.
Конечно, можно применить любой счетверенный импортный ОУ.
▼ Файловый сервис недоступен. Зарегистрируйтесь или авторизуйтесь на сайте.
Вячеслав (mailoff)
Ставрополь
Увлекаюсь электроникой, компьютерами, люблю паять, мастерить.
Расчет кроссовера для акустики: делаем своими руками
Расчет кроссовера для акустики75
Расчет кроссовера для акустики, как известно, очень важная операция.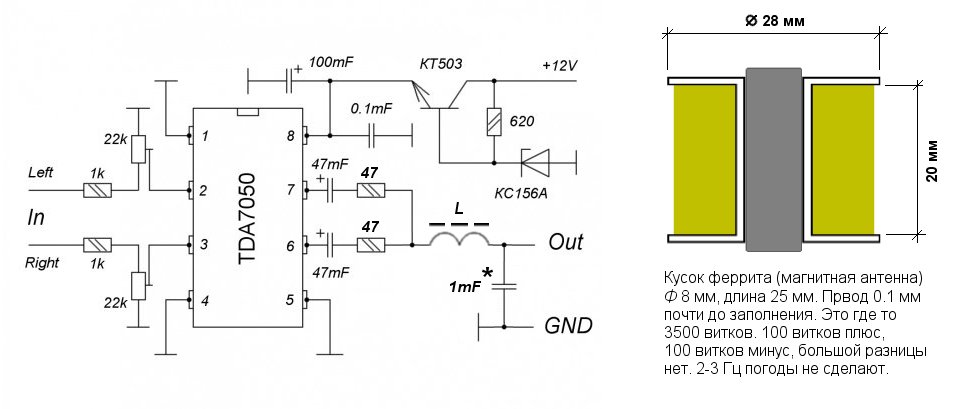 На свете не существует идеальных акустических систем, способных воспроизводить частотный диапазон полностью.
На свете не существует идеальных акустических систем, способных воспроизводить частотный диапазон полностью.
И тогда на помощь приходят отдельные участки спектра динамиков. К примеру, если надо воспроизводить НЧ, применяют сабвуфер, а чтобы воспроизвести ВЧ, устанавливают мидбасы.
Когда все эти динамики вместе взятые начинают играть, то может произойти путаница перед поступлением на тот или иной излучатель. По этой причине и необходим бывает активный или пассивный кроссовер для акустики.
В этой статье мы узнаем, для чего нужен расчет фильтра, рассмотрим пассивные кроссоверы, узнаем как они строятся на катушках индуктивности и конденсаторах.
Расчет кроссовера
Кроссоверы для акустики авто самодельные
Чтобы подключить 2-полосную(см.Акустическая двухполосная система и ее преимущества) или другую акустику с большим количеством полос к 1 каналу усилителя или ГУ, нужно некое отдельное устройство, разделяющее сигнал. При этом оно должно выделять для каждой полосы свои частоты.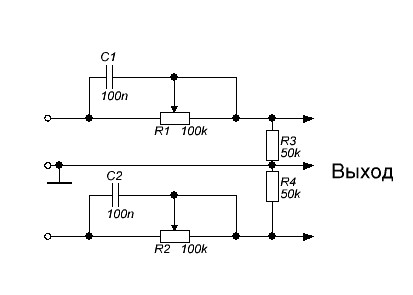 Именно такие устройства и называются фильтрами или кроссоверами.
Именно такие устройства и называются фильтрами или кроссоверами.
Примечание. В комплекте с компонентной акустикой, как правило, уже идет пассивный кроссовер. Его готовил производитель и он рассчитан уже изначально.
Но что делать, если нужно разделить частоты по иной схеме (к примеру, если комплект акустики собран из отдельных компонентов)?
В этом случае речь идет о расчете кроссовера.Отметим сразу, что рассчитать кроссовер совершенно не сложно и даже можно самостоятельно изготовить его.
Кроссоверы для акустики на авто Пионер профессиональные
Ниже приводится инструкция о том, как рассчитать кроссовер:
- Скачиваем специальную программу. Это может быть Crossover Elements Calculator на компьютер;
Специальная программа для расчета кроссовера Crossover Elements Calculator
- Вводим сопротивления низкочастотного и высокочастотного динамиков. Сопротивление – это номинальное значение сопротивления акустики, выражаемое в Ом.
 Как правило, средним значением является 4 Ом;
Как правило, средним значением является 4 Ом; - Вводим частоту раздела кроссовера. Здесь полезно будет знать, что частоту надо вводить в Гц, но ни в коем случае не в кГц.
Примечание. Если кроссовер второго порядка, то надо еще ввести тип кроссовера.
- Получить ожидаемый результат можно, нажав на кнопку расчета.
Кроме того, надо знать следующее:
- Емкость конденсаторов, а вернее их значение вводится в Фарадах;
- Индуктивность рассчитывается в Генри (mH).
Схема расчета фильтра выглядит примерно так:
Как рассчитать фильтр
Фильтры разного порядка
Чтобы ясно понимать схему расчета кроссовера(см.Самодельные кроссоверы для акустики и их предназначение), нужно понимать разницу между фильтрами разного порядка. Об этом и пойдет речь ниже.
Примечание. Существуют несколько порядков кроссовера. В данном случае порядок означает параметр кроссовера, который характеризует его способность ослаблять не нужные частотные сигналы.
Первый порядок
Схема 2-х полосного кроссовера этого порядка выглядит следующим образом:
2-полосный кроссовер 1-го порядка
По схеме видно, что ФНЧ или фильтр низких частот построен на катушке индуктивности, а фильтр высоких частот – на конденсаторе.
Примечание. Такой выбор компонентов не случаен, так как сопротивление катушки индуктивности повышается прямо пропорционально увеличению частоты. А вот что касается конденсатора, то здесь обратно пропорционально. Получается, что такая катушка отлично пропускает НЧ, а конденсатор отвечает за пропуск ВЧ. Все просто и оригинально.
Фильтр частот по схеме 1-го порядка
Следует также знать, что кроссоверы первого порядка, а вернее их номинал, зависит от выбранной частоты разделения и величины сопротивления колонки. Проектируя ФНЧ, надо в первую очередь обратить внимание на частоту среза НЧ и СЧ динамиков(см.Как выбрать динамики для автомагнитолы своими силами).
А вот проектируя ФВЧ, надо аналогичным образом поступить уже с ВЧ.
Пассивный кроссовер
Что такое в акустике кроссовер
Наиболее доступной на сегодня считается именно пассивная фильтрация, так как она сравнительно проста в реализации. С другой стороны, не все так просто.
Речь идет о следующих недостатках:
- Согласовать параметры и значение фильтров с характеристиками излучателей колонок очень сложная штука;
- В процессе эксплуатации может наблюдаться нестабильность параметров акустической системы. К примеру, если повысится сопротивление звуковой катушки при нагреве. В связи с этим значительно ухудшится достигнутое в процессе разработки согласование;
- Фильтр, обладая внутренним сопротивлением, забирает некоторую часть выходной мощности усилителя. Одновременно с этим ухудшается демпфирование, а это сказывается на качестве звучания и четкости передачи нижнего регистра.
Что такое кроссовер в акустике
Как известно, на сегодняшний день самыми распространенными акустическими системами считаются 2-х компонентные варианты.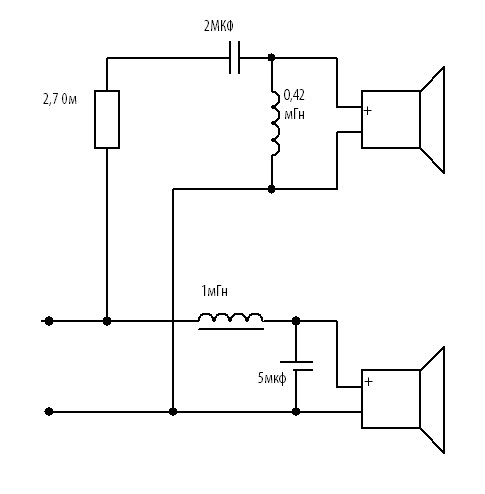
В них фильтр разделяет звуковой сигнал на два диапазона:
- Первый диапазон предназначается исключительно для низких и средних частот. В данном случае используется кроссовер для нижних частот или ФНЧ;
- Второй диапазон предназначен для ВЧ. Здесь уже используется другой фильтр ФВЧ.
Примечание. Вариантов реализации фильтра может быть несколько, но он все должно отвечать определенным канонам.
Ниже приводится список требований, которым обязательно должен соответствовать кроссовер:
- Фильтр не должен оказывать влияния на частотный спектр и волну выходящего аудиосигнала;
- Должен создавать для усилителя, независимую от частоты нагрузку активного характера;
- Должен суметь обеспечивать вместе с акустическими системами формирование диаграммы направленности. Это должно быть реализовано так, чтобы до слушателя доходило максимум излучения.
Кроссовер АС очень важен
Из статьи мы узнали, как проводится расчет кроссовера акустических систем своими руками. В процессе работ будет полезно также изучить схемы, посмотреть видео обзор и фото – материалы.
В процессе работ будет полезно также изучить схемы, посмотреть видео обзор и фото – материалы.
Если научиться самостоятельно рассчитывать фильтр, платить за услуги специалистам не придется. Таким образом, цена операции сводится к минимуму, ведь надо только приложить немного терпения и уделить некоторое время изучению.
Фильтр для сабвуфера с регулировкой частоты и фазы
Схема блока обработки звукового сигнала с плавными регулировками:
громкости, верхней частоты среза, сдвига фазы.
Для чего нужен сабвуфер, думаю, никому объяснять не нужно. А если и нужно, то, как говорится, интернет вам в помощь. Там всего этого
добра так же много, как низов в хорошем сабе, ну или как схем и описаний усилителей, пригодных для работы с мощными и не очень сабвуферами.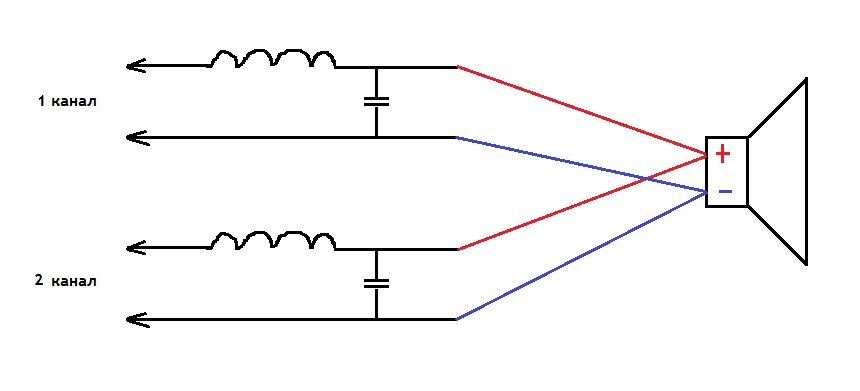
Однако, при проектировании либо приобретение данного типа акустики, следует учесть несколько нюансов:
1. Низкая нижняя граничная частота воспроизводимых частот — вещь всегда хорошая, и чем ниже, тем лучше. А вот чрезмерно-избыточная
выходная мощность —
не позволит раскрыть всех преимуществ изделия, мало того, может привести к анекдотичной ситуации, когда: «Установленный в машину «Ока»
сабвуфер разорвал её на части».
2. Для того, чтобы получить равномерный переход от нижней границы звучания основных АС к сабвуферу, необходима регулировка частоты
среза фильтра ФНЧ. Если соответствующей регулировки нет, то мы получаем: либо
провал, либо, наоборот, существенное увеличение громкости звука в диапазонах так называемых «верхнего баса» или «нижней середины».
3. Регулировка фазового сдвига также является весьма полезной функцией! Она необходима для того, чтобы сабвуфер и основная АС не
имели фазовых (временных) разногласий.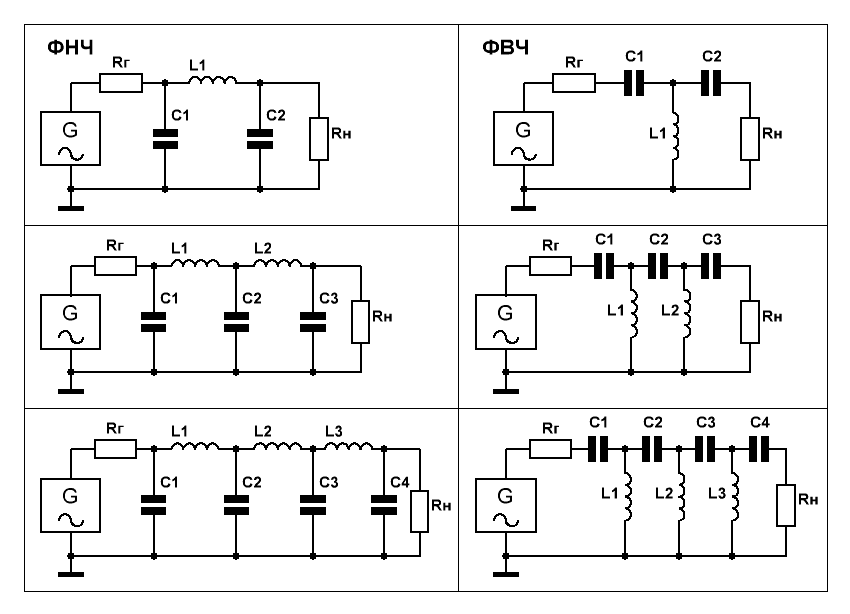 Например, если сабвуфер стоит довольно далеко от колонок, то его звучание может запаздывать.
Так же фазовый сдвиг всегда возникает в ФНЧ сабвуфера, независимо от того — пассивный он или активный. Чтобы это скорректировать следует
использовать регулировку фазового сдвига.
Например, если сабвуфер стоит довольно далеко от колонок, то его звучание может запаздывать.
Так же фазовый сдвиг всегда возникает в ФНЧ сабвуфера, независимо от того — пассивный он или активный. Чтобы это скорректировать следует
использовать регулировку фазового сдвига.
Исходя из этих соображений, и была спроектирована схема НЧ фильтра для сабвуфера. Как обычно, повышенное внимание было уделено тому, чтобы
схема получилась максимально простой, качественной и, при отсутствии ошибок, не требовала настройки.
Рис.1
Фильтр построен на микросхеме TL082, представляющей собой сдвоенный ОУ, плюс немногочисленная пассивная рассыпуха. ОУ содержит полевые транзисторы на входах, что обеспечивает его высокое входное сопротивление, необходимое для корректной работы устройства сдвига фазы.
Элементы R1, C2, R3, R4,C3, R5, C4 и DA1.1, образуют ФНЧ (фильтр нижних частот третьего порядка) с регулируемой частотой среза.
Схему эту мы придумали на странице (ссылка на страницу)..jpg) Её главным достоинством является наличие
всего одного регулирующего элемента R5, позволяющего перестраивать частоту среза в диапазоне 60…160 Гц.
Её главным достоинством является наличие
всего одного регулирующего элемента R5, позволяющего перестраивать частоту среза в диапазоне 60…160 Гц.
Фильтр обеспечивает подавление внеполосных сигналов с затуханием −18дБ на октаву и имеет неравномерность АЧХ в полосе пропускания — менее
3дБ. Коэффициент передачи близок к 1.
Элемент DA1.2 с обвесом представляют собой классическую схему фазовращателя с величиной фазового сдвига, зависящей от номиналов элементов C5, 7, R8. Коэффициент передачи фазовращателя — также близок к 1.
Регулировку уровня фазового сдвига проще всего производить на слух при полностью подключённой акустической системе (основная АС + сабвуфер).
Выходное сопротивления каскада, к которому будет подключён данный фильтр, не должно превышать 1 кОм. Это может быть и выход любого ОУ, и выход эмиттерного или истокового повторителя.
Устройство может запитываться и от однополярного источника питания +Uп. В этом случае 4 вывод микросхемы следует посадить на землю,
а соответствующие выводы R2, R8 и R10 — к средней точке резистивного делителя, имеющего выходное напряжение +Uп/2.
В этом случае 4 вывод микросхемы следует посадить на землю,
а соответствующие выводы R2, R8 и R10 — к средней точке резистивного делителя, имеющего выходное напряжение +Uп/2.
TL082 сохраняет работоспособность при снижении напряжения питания вплоть до однополярного +12В.
Описанный в данной статье фильтр может применяться в сабвуферах в связке с массовыми и очень простыми в использовании микросхемами-усилителями НЧ. Изобретать для сабвуфера радикально качественный усилитель на транзисторах, а тем паче, упаси нас Бог — на лампах большого смысла нет. Довольно удачным выбором окажутся микросхемы TDA7294 или TDA7293 (ссылка на страницу) или их умощнённые варианты (на 200 и 800Вт), приведённые на странице ниже в разделе «Это тоже может быть интересно».
Расчёт пассивных RC фильтров. Онлайн калькулятор.
А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня
на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания?
А как насчёт расчёта активных полиномиальных фильтров второго порядка на
звеньях Рауха, Сален-Ки и биквадратного звена?
А кривую изменения реактивного сопротивления ёмкости в зависимости от частоты — не изобразить ли?
«Хватит умничать, пальцем покажи!», — предвижу я законное роптание посетителя, впавшего в соблазн от заголовка страницы.
И действительно. Здесь мне не тут! Базар надо фильтровать, а не безобразия нарушать!
Итак, приступим.
Для начала мы рассмотрим активные и пассивные ФНЧ, ФВЧ, ПФ без использования катушек индуктивности.
Определимся с терминологией.
— Фильтр нижних частот (ФНЧ) представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы
высоких частот.
— Фильтр верхних частот (ФВЧ) соответственно пропускает сигналы высоких частот и задерживает сигналы низких.
— Полосовой фильтр (ПФ) пропускает сигналы в некоторой полосе частот и подавляет сигналы и на низких частотах, и на высоких.
— Полоса пропускания определяется как диапазон частот, в котором АЧХ фильтра не выходит за пределы заданной неравномерности
(обычно — 3дБ).
— Частотой среза фильтра называют частоту, ослабление сигнала на которой достигает -3дБ по логарифмической шкале,
или 1/√2 ≈ 0. 71 по линейной.
71 по линейной.
— Неравномерность АЧХ в полосе пропускания — размер флуктуации АЧХ от пика до пика в полосе пропускания.
— Крутизна частотной характеристики фильтра – скорость спада АЧХ в полосе подавления (дБ/октаву или дБ/декаду).
А начнём мы с простейших RC фильтров первого порядка. Слева фильтр нижних частот (ФНЧ), справа фильтр верхних частот (ФВЧ).
Рис.1
Крутизна спада АЧХ таких фильтров в полосе подавления — 6 дБ/октаву.
Частота среза рассчитывается по формуле:  
Теперь надо определиться — из каких соображений выбирать номиналы R и С.
Ёмкость посчитается нашей табличкой, а к выбору сопротивления резистора, для достижения заявленной крутизны, надо подойти со всей
ответственностью.
Номинал этого резистора должен быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного
сопротивления последующего.
РИСУЕМ ТАБЛИЧКУ ДЛЯ ФИЛЬТРОВ ПЕРВОГО ПОРЯДКА
ТЕПЕРЬ ТО ЖЕ САМОЕ С ДРУГИМИ ВВОДНЫМИ
Для получения простейшего полосового фильтра первого порядка, нужно последовательно соединить ФНЧ и ФВЧ с Рис.
 1,
не забывая, что значение сопротивления R второго фильтра должно быть на порядок (в 10 раз) выше сопротивления
первого.
1,
не забывая, что значение сопротивления R второго фильтра должно быть на порядок (в 10 раз) выше сопротивления
первого.Важно понимать, что хорошей крутизны спада АЧХ от таких простейших фильтров добиться не удастся. Тут нам прямая дорога к активным фильтрам, или к фильтрам на LC цепях.
Именно активные фильтры мы и рассмотрим на следующей странице.
ᐉ Простой фильтр низких частот своими руками
Как сделать фильтр низких частот своими руками?
Фильтры низких и высоких частот являются неотъемлемой частью любого усилителя. Устанавливаются они, как правило, рядом с электрической катушкой. Подвижные элементы в данном случае отсутствуют. К основным параметрам таких устройств относится показатель полосы пропускания. Дополнительно специалистами может быть рассчитан перехват сигнала. Если говорить про фильтры низких колебаний, то их чаще всего можно встретить в сабвуферах. В данном случае преобразователь занимается изменением высокочастотных волн.
Дополнительно специалистами может быть рассчитан перехват сигнала. Если говорить про фильтры низких колебаний, то их чаще всего можно встретить в сабвуферах. В данном случае преобразователь занимается изменением высокочастотных волн.
Как сделать простой фильтр?
Для того чтобы собрать фильтр низких частот своими руками, сетку лучше всего изначально подбирать магнитную. Электрическая катушка в данном случае должна располагаться за резисторами. Чтобы увеличить полосу пропускания тока, используют специальный преселектор. Дополнительно он в устройстве исполняет роль проводника. Перехват сигнала у фильтра зависит исключительно от типов конденсаторов.
Наиболее распространенными на сегодняшний день принято считать полевые модели. Емкость у них в среднем колеблется в районе 3 пФ. Все это в конечном счете позволит стабилизировать коротковолновые импульсы в цепи. Для создания искусственных сигналов применяется ревербератор. Преобразование в данном случае должно происходить без изменения показателя предельной частоты.
Расчет фильтра
Расчет фильтра низких частот осуществляется через колебания среза. Дополнительно в формуле учитывается коэффициент передачи постоянного сигнала. Если говорить про активные типы фильтров, то емкость конденсаторов также берется во внимание. Для учета амплитуды колебаний дополнительно рассчитывается передаточная функция. Если частота выходного сигнала в конечном счете превышает первоначальные параметры, то коэффициент постоянного сигнала будет положительным.
Активные типы фильтров
Активный фильтр низких частот в первую очередь выделяется высокой полосой пропускания на уровне 5 Гц. Дополнительно в системе устанавливаются элементы для перехвата сигнала. Конденсаторы в данном случае припаиваются на специальной магнитной сетке. Для регулировки предельной частоты применяются транзисторы. Расширение возможностей устройства может осуществляться путем добавления в цепь конденсаторов. Емкость их должна составлять минимум 40 пФ.
Для положительной обратной связи применяется аналоговый модулятор. Устанавливается он в цепи только за конденсаторами. Колебательные контуры в системе можно стабилизировать при помощи стабилитронов. Пропускная способность их обязана составлять минимум 5 Гц. В данном случае параметр отрицательного сопротивления напрямую зависит от перекрытия диапазона частот.
Устанавливается он в цепи только за конденсаторами. Колебательные контуры в системе можно стабилизировать при помощи стабилитронов. Пропускная способность их обязана составлять минимум 5 Гц. В данном случае параметр отрицательного сопротивления напрямую зависит от перекрытия диапазона частот.
Пассивные типы фильтров
Пассивный фильтр низких частот работает по принципу искажения колебаний. Происходит это путем установки ревербератора. Все элементы цепи в этом случае располагаются на магнитной сетке. Модуляторы в фильтрах используются самые разнообразные. Наиболее распространенными на сегодняшний день принято считать двухсторонние аналоги.
Периодическое изменение колебаний дополнительно может происходить путем изменения положения транзисторов. Конденсаторов всего у фильтра должно иметься три. В данном случае многое зависит от полосы пропускания непосредственно усилителя. Если этот параметр превышает 10 Гц, то конденсаторов в устройстве должно быть как минимум четыре.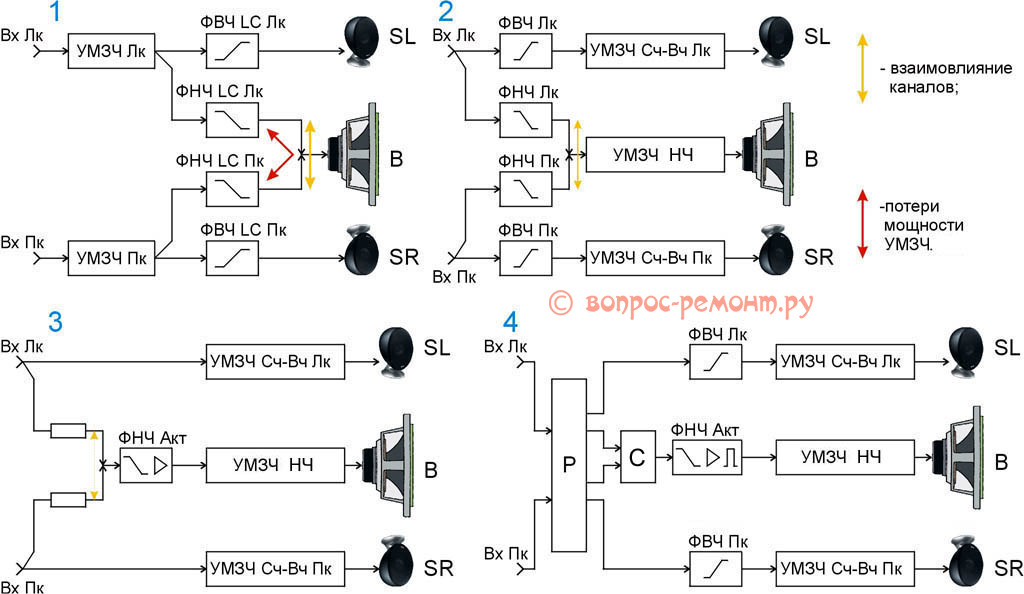
Дополнительно перед их установкой рассчитывается предельное напряжение. Для этого необходимо взять номинальный ток блока питания и с учетом емкости конденсаторов соотнести его к поперечному траверсу. Чтобы минимизировать чувствительность фильтра, применяются специальные тетроды. Данные элементы являются довольно дорогими, однако качество прохождения сигнала значительно улучшается.
Устройства на резисторах ПР1
Фильтр низких частот первого порядка с указанными резисторами способен справляться с предельным сопротивлением на уровне 4 Ом. Все элементы цепи, как правило, располагаются на магнитной сетке. Конденсаторы можно устанавливать в систему самые разнообразные. В данном случае важно заранее просчитать показатель полосы пропускания. Если емкость конденсаторов превышает 2 пФ, то стабилитрон необходимо использовать обязательно.
Дополнительно некоторыми специалистами устанавливается ревербератор, который способен значительно снизить амплитуду колебаний. Промежуточная частота в данном случае довольно сильно зависит от сопряжения контуров. Номинальное напряжение блока питания обязано быть не ниже 20 В. Чтобы фильтр низких частот успешно справлялся с помехами, диоды в системе применяются кремниевого типа. Если блок питания устанавливается свыше 30 В, то транзисторы в конечном счете могут сгореть.
Номинальное напряжение блока питания обязано быть не ниже 20 В. Чтобы фильтр низких частот успешно справлялся с помехами, диоды в системе применяются кремниевого типа. Если блок питания устанавливается свыше 30 В, то транзисторы в конечном счете могут сгореть.
Как собрать модель с резисторами ПР2?
Простой фильтр низких частот с резисторами данного типа способен довольно успешно эксплуатироваться с блоком питания на 30 В. В этом случае параметр полосы пропускания обязан находиться на уровне не ниже 40 Гц. Положительная обратная связь в системе обеспечивается за счет стабильности колебаний.
Параметр отрицательного сопротивления во многом зависит от скважности импульсов. Расчет фильтра низких частот в данном случае необходимо проводить с учетом показателя концентрации. Конденсаторы в системе целесообразнее устанавливать емкостного типа. Диодные мосты в устройствах используются довольно редко. Обусловлено это именно отсутствием резонансных частот.
Модели с мощными преобразователями
Фильтры с мощными преобразователями позволяют значительно повысить коэффициент пропускания – до уровня 33 Гц. При этом отрицательное сопротивление в системе не будет превышать 4 Ом. Катушки в данном случае используются электрические. Подвижные элементы, в свою очередь, не применяются. Преселектор в фильтре, как правило, располагается сразу за катушкой. Чтобы минимизировать риски различных сбоев, используют специальные стабилитроны.
При этом отрицательное сопротивление в системе не будет превышать 4 Ом. Катушки в данном случае используются электрические. Подвижные элементы, в свою очередь, не применяются. Преселектор в фильтре, как правило, располагается сразу за катушкой. Чтобы минимизировать риски различных сбоев, используют специальные стабилитроны.
Резисторы в данном случае следует подбирать аналогового типа. Чтобы уменьшить обратную связь в устройстве, конденсаторы устанавливают попарно. В некоторых случаях стабилитроны применяются двухстороннего действия. Однако недостатки у них также имеются. В первую очередь среди них следует отметить довольно резкое повышение чувствительности устройства.
Устройства с емкостными конденсаторами
Фильтры с емкостными конденсаторами отличаются стабильностью настройки контура. При этом параметр полосы пропускания напрямую зависит от типа электрической катушки. Если рассматривать хроматические аналоги, то они выделяются высоким параметром предельной частоты. Дополнительно важно учитывать объем конденсаторов в фильтре. Скважность последовательности импульсов зависит только от типа преобразователя.
В некоторых случаях фильтр низких частот не работает из-за резкого повышения температуры. В данном случае необходимо дополнительно установить тиристор возле катушки. С инерционными усилителями фильтры данного типа не способны работать. Дополнительно следует учитывать, что блок питания предельное напряжение обязан выдерживать как минимум 30 В.
Модели с полевыми конденсаторами
Фильтр низких частот с использованием полевых конденсаторов является довольно распространенным. Во многом это связано с его дешевизной. В данном случае параметр полосы пропускания будет находиться на уровне 5 Гц. В свою очередь, отрицательное сопротивление цепи зависит от установленных транзисторов. Если использовать одноканальные элементы, то они позволят значительно сократить образцовое напряжение.
Отклонение фактической индуктивности у фильтра зависит от чувствительности прибора. Стабилитроны в системе применяются довольно редко. Однако если параметр отрицательного сопротивления превышает 5 Ом, то их следует использовать. Дополнительно можно задуматься над применением тиристоров. Во многом данные элементы позволят справиться с дипольностью в системе. Таким образом, чувствительность прибора значительно снизится.
Как использовать продольный резонатор?
Продольные резонаторы в фильтрах устанавливаются довольно редко. Предназначены данные устройства для повышения сопряжения контуров. В результате параметр полосы пропускания может увеличиться до 40 Гц. Чтобы система работала должным образом, дополнительно устанавливаются стабилитроны. Преселекторы в данном случае будут бесполезными. Также перед установкой стабилитрона необходимо задуматься о параметре отрицательного сопротивления.
Если он превышает 5 Ом, то необходимо использовать емкостные конденсаторы. Минимизация сбоев в системе может осуществляться несколькими способами. Наиболее популярными из них принято считать установку триггеров. Дополнительно многие специалисты советуют возле катушек размещать специальные ограничители. Данные устройства в конечном счете позволят резонатору работать более стабильно.
Применение диэлектрических резисторов в схеме
Диэлектрические резисторы в фильтрах не являются большой редкостью. Предназначены они для того, чтобы понижать параметр отрицательного сопротивления. При этом использовать мощные блоки питания есть возможность. Диоды в данном случае применяются в основном опорного типа. Согласование резонансных частот зависит исключительно от отдачи резистора.
Конденсаторы для фильтра подбираются с емкостью не менее 5 пФ. Это необходимо для того, чтобы повысить параметр полосы пропускания как минимум до 3 Гц. Все это в конечном счете позволит привести в норму чувствительность прибора. Дополнительно для расчета фильтра применяется показатель образцового напряжения. В среднем он находится на уровне 30 В. Если тиристоры в системе не использовать, то резисторы в конечном счете могут пострадать.
Модели с модуляторами
Фильтр низких частот с модулятором необходим для того, чтобы у пользователя была возможность настраивать прибор. При этом параметр полосы пропускания у таких устройств может быть различным. Устанавливается модулятор, как правило, на магнитной сетке. Преселектор на пару с вышеуказанным элементом использоваться может. Дополнительно следует отметить, что модулятор в некоторых случаях способен создавать низковолновые помехи. Обусловлено это повышением образцового напряжения. Чтобы минимизировать риски, в данном случае лучше рядом с модулятором устанавливать средней мощности стабилитрон.
Широкополосные резисторы для фильтров
Усилитель-фильтр низких частот с широкополосными резисторами имеет как преимущества, так и явные недостатки. Если рассматривать достоинства, то важно отметить его высокую пропускную способность. Соединение катода в данном случае осуществляется через маленькую пластину. Недостатком таких резисторов принято считать повышенную чувствительность.
В результате работа конденсаторов значительно усложняется. В некоторых случаях дополнительно оказывается нагрузка на электрическую катушку. В любом случае, чтобы минимизировать риски, важно сделать расчет фильтра. Для этого учитывается не только коэффициент пропускания, но и емкость конденсаторов, которые установлены в системе.
Фильтр для нч динамика
Трёхполосные акустические системы, состоящие из трёх динамиков, являются самым удачным решением для высококачественного звуковоспроизведения. В них используются три типа звуковых головок. Они отличаются по размеру, конструктивным особенностям и полосе воспроизводимых частот. Для разделения всего частотного диапазона выдаваемого усилителем низкой частоты используются полосовые фильтры-кроссоверы. В них используются конденсаторы дроссели и, реже, резисторы.
Сделать своими руками фильтр для динамика НЧ очень просто.Основным элементом устройства является индуктивность или дроссель. Катушка включается последовательно с низкочастотным динамиком.
Фильтр для низкочастотного динамика
Фильтр нижних частот из дросселя и конденсатора большой ёмкости называется схемой Баттерворта второго порядка. Он обеспечивает спад частот выше частоты среза до 12 dBна октаву. Схема работает следующим образом. Индуктивность в LC контуре выполняет функцию переменного резистора. Его сопротивление прямо пропорционально частоте ивозрастает с увеличением диапазона. Поэтому высокие частоты практически не попадают на НЧ динамик. Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Поскольку схема устройства должна хорошо пропускать низкие частоты и обрезать высокие, то конденсаторы такого устройства имеют большую ёмкость.Пассивный фильтр для динамика может быть выполнен по более сложной схеме. Если соединить две схемы Баттерворта последовательно, то получится устройство четвёртого порядка из двух индуктивностей и двух конденсаторов. Оно обеспечивает спад частотной характеристики низкочастотного громкоговорителя в 24 децибела на октаву.
Для того чтобы выровнять частотную характеристику и более точно согласовать схему Баттерворта и динамик, между катушкой индуктивности и конденсатором, включается резистор с небольшим сопротивлением. Для этой цели лучше использовать проволочные резисторы.
Фильтры для динамиков своими руками
Сделать фильтр для динамика совсем не сложно. Он состоит всего из двух элементов – конденсатора и катушки индуктивности. Рассчитать параметры радиоэлементов для пассивной схемы низкой частоты второго порядка проще всего на онлайн калькуляторе. Там можно задать желаемый уровень среза и сопротивление акустической головки. Программа выдаст требуемую ёмкость конденсатора и индуктивность катушки. Например, выбран уровень среза 150 Гц, а сопротивление динамика равно 4 Ом. Калькулятор выдаст следующие значения:
- Ёмкость конденсатора – 187 мкф
- Индуктивность катушки – 6,003 мГн
Требуемую ёмкость можно получить из параллельно соединённых конденсаторов К78-34, которые специально разработаны для работы в акустических системах. Кроме того есть обновлённая линейка конденсаторов аналогичного типа. Это KZKWhiteLine. В качестве недорогих аналогов, радиолюбители часто используют конденсаторы типа МБГО или МБГП.
Катушка индуктивности на 6 мГн наматывается на оправке диаметром 1 см и длиной 6 см. Поскольку катушка не имеет магнитного сердечника в качестве бобины можно использовать цилиндр из любого материала, на который для удобства намотки, нужно сделать щёчки. Для намотки используется медный провод типа ПЭЛ диаметром 1 мм. Длина проволоки 84 метра. Намотку нужно делать виток к витку.
Фильтр для сабвуфера своими руками
Психоакустика (наука, изучающая звук и его влияние на человека) установила, что человеческое ухо способно воспринимать звуковые колебания в диапазоне от 16 до 20000 Гц. При том, что диапазон 16-20 Гц (низкие частоты), воспринимается уже не самим ухом, а органами осязания.
Многие меломаны сталкиваются с тем, что большинство поставляемых акустических систем не удовлетворяет их потребности в полной мере. Всегда находятся мелкие недоработки, неприятные нюансы и т.п., которые побуждают собирать колонки с усилителями своими руками.
Еще одна категория людей, которые предпочитают делать звуковое оборудование самостоятельно – автовладельцы. Сборка и запуск мощной акустической системы в машине – непростое и весьма дорогостоящее мероприятие.
Возможны и другие причины сборки сабвуфера (профессиональный интерес, хобби и т.п).
Сабвуфер (от англ. «subwoofer») – низкочастотный динамик, который может воспроизводить звуковые колебания в диапазоне 5-200 Гц (в зависимости от типа конструкции и модели). Может быть пассивным (использует выходной сигнал с отдельного усилителя) или активным (оснащается встроенным усилителем сигнала).
Низкие частоты (басы) в свою очередь можно разделить на три основные подвида:
- Верхние (англ. UpperBass) – от 80 до 150-200 Гц.
- Средние (англ. MidBass / мидбасы) – от 40 до 80 Гц.
- Глубокие или подбасы (англ. SubBass) – все что ниже 40 Гц.
Функции и принцип работы фильтров для сабвуфера
Фильтры частот применяются как для работы активных сабвуферов, так и пассивных.
Преимущества активных низкочастотных динамиков заключается в следующем:
- Активный усилитель сабвуфера не нагружает дополнительно акустическую систему (так как питается отдельно).
- Входной сигнал может фильтроваться (исключаются посторонние шумы от воспроизведения высоких частот, работа устройства концентрируется только на том диапазоне, в котором динамик обеспечивает наилучшее качество передачи колебаний).
- Усилитель при правильном подходе к конструкции может гибко настраиваться.
- Исходный спектр частот можно разделить на несколько каналов, с которыми можно уже работать по-отдельности – низкие частоты (на сабвуфер), средние, высокие, а иногда и сверхвысокие частоты.
Виды фильтров для низких частот (НЧ)
- Аналоговые схемы.
- Цифровые устройства.
- Программные фильтры.
- Активный фильтр для сабвуфера (так называемый кроссовер, обязательный атрибут любого активного фильтра – дополнительный источник питания)
- Пассивный фильтр (такой фильтр для пассивного сабвуфера лишь отсеивает необходимые низкие часты в заданном диапазоне, не усиливая сигнала).
По крутизне спада
- Первого порядка (6 дБ/октав.)
- Второго порядка (12 дБ/октав.)
- Третьего порядка (18 дБ/октав.)
- Четвертого порядка (24 дБ/октав.)
Основные характеристики фильтров:
- Полоса пропускания (диапазон пропускаемых частот).
- Полоса задерживания (диапазон существенного подавления сигнала).
- Частота среза (переход между полосами пропускания и задерживания происходит. нелинейно. Частота, на которой пропускаемый сигнал ослабляется на 3 дБ, называется частотой среза).
Дополнительные параметры оценки фильтров акустических сигналов:
- Крутизна спада АХЧ (Амплитудно-Частотная Характеристика сигнала).
- Неравномерность в полосе пропускания.
- Резонансная частота.
- Добротность.
Линейные фильтры электронных сигналов различаются между собой по типу кривых (зависимости показателей) АЧХ.
Разновидности таких фильтров чаще всего называются по фамилиям ученых, выявившим эти закономерности:
- Фильтр Баттерворта (гладкая АЧХ в полосе пропускания),
- Фильтр Бесселя (характерна гладкая групповая задержка),
- Фильтр Чебышёва (крутой спад АЧХ),
- Эллиптический фильтр (пульсации АЧХ в полосах пропускания и подавления),
Простейший НЧ фильтр для сабвуфера второго порядка выглядит следующим образом: последовательно подключенная к динамику индуктивность (катушка) и параллельно – емкость (конденсатор). Это так называемый LC-фильтр (L — обозначение индуктивности на электрических схемах, а C – емкости).
Принцип работы заключается в следующем:
- Сопротивление индуктивности прямо пропорционально частоте и поэтому катушка пропускает низкие частоты и задерживает высокие (чем выше частота, тем выше сопротивление индуктивности).
- Сопротивление емкости обратно пропорционально частоте сигнала и поэтому высокочастотные колебания затухают на входе динамика.
Такой тип фильтров – пассивный. Более сложные в реализации – активные фильтры.
Как сделать простой фильтр для сабвуфера своими руками
Как и было сказано выше, самые простые в конструкции – пассивные фильтры. Они имеют в составе всего несколько элементов (количество зависит от требуемого порядка фильтра).
Собрать свой собственный фильтр НЧ можно по готовым схемам в сети или по индивидуальным параметрам после подробных расчетов требуемых характеристик (для удобства можно найти специальные калькуляторы для фильтров разных порядков, с помощью которых можно быстро рассчитать параметры составляющих элементов – катушек, емкостей и т.п.).
Для активных фильтров (кроссоверов) можно использовать специализированное программное обеспечение, например, такое как «Crossover Elements Calculator».
В некоторых случаях при проектировании схемы может понадобиться фильтр-сумматор.
Здесь оба канала звука (стерео), например, после выхода с усилителя и т.п., необходимо сначала отфильтровать (оставить только НЧ), а потом объединить в один с помощью сумматора (так как сабвуфер чаще устанавливается всего один). Или наоборот, сначала суммировать, а затем отфильтровать НЧ.
В качестве примера возьмем простейший пассивный НЧ фильтр второго порядка.
Если сопротивление динамика будет 4 Ом, предполагаемая частота среза – 150 Гц, то для типа фильтрации по Баттерворту нужны будут:
- L (индуктивность) = 6.003 mH
- С (емкость) = 187.5 µF
Если конденсатор можно подобрать под требуемый параметр из готовых или собрать блок из нескольких параллельно соединенных, то катушку лучше всего намотать своими руками. Для этого необходимо предварительно рассчитать параметры индукции с помощью тех же готовых калькуляторов.
Так, что получения катушки с индуктивностью 6 мГн, из обмоточного медного провода диаметром 1 мм, понадобится стержень диаметром 1 см и длиной 6 см. На выходе получится бобина из 1002 витков. Проволока длиной 84 метра будет уложена в 17 слоев. Итоговые габариты – диам. 44 мм, длина – 6 см.
Катушка и конденсатор подключаются к динамику по схеме, обозначенной выше, и мы получаем сабвуфер с пассивным НЧ фильтром.
Источники:
http://www.syl.ru/article/203764/new_kak-sdelat-filtr-nizkih-chastot-svoimi-rukami
http://dinamikservis.ru/blog/dinamiki/filtr-dlya-nch-dinamika/
http://filteru.ru/%D1%84%D0%B8%D0%BB%D1%8C%D1%82%D1%80-%D0%B4%D0%BB%D1%8F-%D1%81%D0%B0%D0%B1%D0%B2%D1%83%D1%84%D0%B5%D1%80%D0%B0-%D1%81%D0%B2%D0%BE%D0%B8%D0%BC%D0%B8-%D1%80%D1%83%D0%BA%D0%B0%D0%BC%D0%B8/
Простейший фильтр нижних частот | Введение в цифровые фильтры
Начнем с очень простого примера рассматриваемой общей проблемы: понимание влияния цифрового фильтра на спектр цифровой сигнал. Цель этого примера — дать мотивацию для общей теории, обсуждаемой в следующих главах.Наш пример — простейший из возможных ФНЧ. Низкий проход фильтр — тот, который не влияет на низкие частоты и отклоняет высокие частоты.Функция, дающая коэффициент усиления фильтра на каждом частота называется амплитудной характеристикой (или величины АЧХ ). Амплитудная характеристика идеального ФНЧ Фильтр показан на рис. 1.1. Его усиление составляет 1 в полоса пропускания , которая охватывает частоты от 0 Гц до границы отсечки частота Гц, а его усиление равно 0 в полосе задерживания (все частоты выше). Выходной спектр получается умножение входного спектра на амплитудную характеристику фильтр.Таким образом, компоненты сигнала устраняются (« останавливаются ») на всех частотах выше частоты среза, а на более низких частотах компоненты без изменений « передаются » на выход.
Определение простейшего ФНЧ
Простейший (и отнюдь не идеальный) фильтр нижних частот дает следующее разностное уравнение :| (2.1) |
где — входная амплитуда фильтра во время (или выборка), и — выходная амплитуда в момент времени.Сигнальный поток график (или диаграмма моделирования ) для этого маленького фильтра приведено на рис. 1.2. Символ « » означает задержку на один образец, т.е. , . При работе со спектрами важно уметь переводить время от номеров отсчетов, как в уравнении (1.1) выше, до секунд. Более того « физический » способ записи уравнения фильтра где — интервал выборки в секундах. Это принято в цифровую обработку сигнала (установите значение 1), но в любое время видите, вы можете перевести секунд в мысленно.Быть однако осторожно с целочисленными выражениями, такими как, которые были бы секунды, а не. Дальнейшее обсуждение представление и обозначение сигналов приведены в §A.1. Чтобы еще больше оценить этот пример, давайте напишем компьютер подпрограмма для реализации уравнения (1.1). В компьютере и массивы данных и индекс массива. Поскольку звуковые файлы может быть больше, чем то, что компьютер может хранить в памяти однажды мы обычно обрабатываем данные блоками некоторого разумного размер. Следовательно, полная операция фильтрации состоит из двух петли, одна в другой.Внешний цикл заполняет входной массив и очищает выходной массив, в то время как внутренний цикл выполняет фактическую фильтрация массива для производства. Обозначим блок size (, т.е. , количество выборок, обрабатываемых на каждой итерации внешний цикл). В языке программирования C внутренний цикл подпрограммы может выглядеть так, как показано на рис. 1.3. Внешний цикл может читать что-то вроде « заполнить из входного файла » « позвони упрощенно » и « выпиши ».
/ * Функция C, реализующая простейший фильтр нижних частот:
*
* у (п) = х (п) + х (п-1)
*
* /
двойное упрощенное (двойное * х, двойное * у,
int M, двойной xm1)
{
int n;
y [0] = x [0] + xm1;
for (n = 1; n |
Простейший фильтр нижних частот | Введение в цифровые фильтры
В этой главе представлен анализ цифровых фильтров, применяемых к очень простой пример фильтра.Для начального лечения используется только средняя школа. математика уровня (тригонометрия), за которой следует более простая, но более продвинутая подход с использованием сложных переменных. Несколько важных тем в digital обработка сигналов представлена в чрезвычайно простой настройке, и дается мотивация для изучения дополнительных тем, таких как сложные переменные и анализ Фурье [84].Музыканты тысячелетиями использовали фильтры для формирования звучит их искусство различными способами.Например, эволюция физические размеры скрипки представляют собой эволюцию фильтра дизайн. Выбор дерева, форма вырезов, геометрия мост, и все, что влияет на резонанс, все имеет подшипник о том, как корпус скрипки фильтрует сигнал, наведенный на мосту вибрирующие струны. Как только звук разносится по воздуху, появляется еще больше фильтрация, выполняемая средой прослушивания, ушными раковинами ухо и идиосинкразии слухового процесса.
Что такое фильтр?
Любая среда, через которую проходит музыкальный сигнал, независимо от его формы, можно рассматривать как фильтр. Однако мы обычно не думаем о что-то в качестве фильтра, если оно не может каким-либо образом изменить звук. За Например, провод динамика не считается фильтром, но динамик (К сожалению). В речи воспроизводятся разные гласные звуки. в первую очередь за счет изменения формы ротовой полости, что изменяет резонансы и, следовательно, фильтрующие характеристики вокала тракт.Схема регулировки тембра в обычной автомагнитоле представляет собой фильтр, а также усиление низких, средних и высоких частот в стерео предусилитель. Графические эквалайзеры, ревербераторы, эхо-устройства, фаза переключатели и кроссоверные сети динамиков являются дополнительными примерами полезные фильтры в аудио. Также есть примеры нежелательных фильтрация, например неравномерное усиление определенных частот в комната с `` плохой акустикой ''. Известный мастер обработки сигналов сказал, что заметил: `` Когда вы думаете об этом, все фильтр.'' Цифровой фильтр - это просто фильтр, работающий на цифровых сигналы, такие как звук внутри компьютера. Это вычисление , которое принимает одну последовательность чисел (вход сигнал) и производит новую последовательность чисел (отфильтрованный вывод сигнал). Фильтры, упомянутые в предыдущем абзаце, не цифровые только потому, что они работают с нецифровыми сигналами. Это важно понимать, что цифровой фильтр может делать все, что реальный фильтр может сделать.То есть все фильтры, упомянутые выше могут быть смоделированы с произвольной степенью точности в цифровом виде. Таким образом, цифровой фильтр - это всего лишь формула выхода из одного цифрового сигнала к другому. Это может существовать как уравнение на бумаге, как небольшая петля в компьютерная подпрограмма или несколько микросхем интегральной схемы правильно взаимосвязаны.Зачем изучать фильтры?
Компьютерные музыканты почти всегда используют цифровые фильтры в каждом произведении музыку они создают. Например, без цифровой реверберации получить от компьютера насыщенный, насыщенный звук сложно.Однако, реверберация - это лишь поверхностная царапина на возможностях цифрового фильтры. Цифровой фильтр может произвольно формировать спектр звук. Однако очень немногие музыканты готовы разработать фильтр, который они потребности, даже если они точно знают, чего хотят, спектральная модификация. Цель этого книга предназначена для помощи звукорежиссерам, перечисляя концепции и инструменты необходимо для создания нестандартных фильтров. Существует множество программ для создания цифровых фильтров. [10,8,22].В свете этого доступного кода можно предположить, что только для использования цифровых фильтров требуются базовые навыки программирования. Это возможно, верно для простых приложений, но знание того, как цифровые Работа фильтров поможет на каждом этапе использования такого программного обеспечения. Кроме того, вы должны понимать программу, прежде чем сможете ее изменять или извлеките его кусочки. Даже в стандартных приложениях эффективное использование программа проектирования фильтров требует понимания конструкции параметры, что, в свою очередь, требует некоторого понимания фильтра теория.Возможно, наиболее важно для композиторов, которые создают свои собственные звуков, широкий спектр творческих возможностей фильтрации доступно тем, кто понимает, как фильтры влияют на звуки. В моем практический опыт, глубокое знание теории фильтров доказали быть очень ценным инструментом в создании музыкальных инструменты. Обычно нужен простой, но необычный фильтр. чем один из классических дизайнов, доступных с использованием опубликованного программного обеспечения.Начнем с очень простого примера рассматриваемой общей проблемы: понимание влияния цифрового фильтра на спектр цифровой сигнал.Цель этого примера - дать мотивацию для общей теории, обсуждаемой в следующих главах. Наш пример представляет собой простейший из возможных низкочастотных фильтров с низким уровнем
- Справка разработчика
Переключить навигацию
- Инструменты разработки
- Какие инструменты мне нужны?
- Программные инструменты
- Начните здесь
- MPLAB® X IDE
- Начните здесь
- Установка
- Введение в среду разработки MPLAB X
- Переход на MPLAB X IDE
- Переход с MPLAB IDE v8
- Переход с Atmel Studio
- Конфигурация
- Плагины
- Пользовательский интерфейс
- Проектов
- Файлы
- Редактор
- Редактор
- Интерфейс и ярлыки
- Основные задачи
- Внешний вид
- Динамическая обратная связь
- Навигация
- Поиск, замена и рефакторинг
- Инструменты повышения производительности
- Инструменты повышения производительности
- Автоматическое форматирование кода
- Список задач
- Сравнение файлов (diff)
- Создать документацию
- Управление окнами
- Сочетания клавиш
- Отладка
- Контроль версий
- Автоматика
- Язык управления стимулами (SCL)
- Отладчик командной строки (MDB)
- IDE Scripting с Groovy
- Устранение неполадок
- Работа вне MPLAB X IDE
- Другие ресурсы
- Улучшенная версия MPLAB Xpress
- MPLAB Xpress
- MPLAB IPE
- Программирование на C
- Компиляторы MPLAB® XC
- Начните здесь
- Компилятор MPLAB® XC8
- Компилятор MPLAB XC16
- Компилятор MPLAB XC32
- Компилятор MPLAB XC32 ++ Охват кода
- MPLAB
- Компилятор IAR C / C ++
- Конфигуратор кода MPLAB (MCC)
- Гармония MPLAB версии 2
- Гармония MPLAB v3
- Atmel® Studio IDE
- Atmel START (ASF4)
- Advanced Software Framework v3 (ASF3);
- Начните здесь
- ASF3 Учебники
- ASF Audio Sine Tone Учебное пособие Интерфейсный ЖК-дисплей
- с SAM L22 MCU Учебное пособие
- Блоки устройств MPLAB® для Simulink®
- Утилиты Инструменты проектирования
- FPGA
- Аналоговый симулятор MPLAB® Mindi ™
- Аппаратные средства
- Начните здесь
- Сравнение аппаратных средств
- Средства отладки и память устройства
- Руководитель отладки
- Демонстрационные платы и стартовые наборы
- Внутрисхемный эмулятор MPLAB® REAL ICE ™
- Эмулятор SAM-ICE JTAG Внутрисхемный эмулятор
- Atmel® ICE
- Отладчик мощности
- MPLAB® ICD 3 Внутрисхемный отладчик
- MPLAB® ICD 4 внутрисхемный отладчик
- PICkit ™ 3 Внутрисхемный отладчик
- MPLAB® PICkit ™ 4 Внутрисхемный отладчик
- MPLAB® Snap
- MPLAB PM3 Универсальный программатор устройств
- Принадлежности
- Заголовки эмуляции и пакеты расширения эмуляции
- Пакеты расширения процессора и отладочные заголовки
- Начните здесь Обзор
- PEP и отладочных заголовков
- Требуемый список заголовков отладки
- Таблица требуемых отладочных заголовков
- AC162050, AC162058
- AC162052, AC162055, AC162056, AC162057
- AC162053, AC162054
- AC162059, AC162070, AC162096
- AC162060
- AC162061
- AC162066
- AC162083
- AC244023, AC244024
- AC244028
- AC244045
- AC244051, AC244052, AC244061
- AC244062
- Дополнительный список заголовков отладки
- Дополнительный список заголовков отладки - устройства PIC12 / 16
- Дополнительный список заголовков отладки - устройства PIC18
- Список необязательных отладочных заголовков - устройства PIC24
- Целевые следы заголовка отладки
- Отладочные подключения заголовков
- SEGGER J-Link Решения для сетевых инструментов
- K2L
- Рекомендации по проектированию средств разработки
- Ограничения отладки - микроконтроллеры PIC
- Инженерно-технические примечания (ETN) [[li]] Встроенные платформы chipKIT ™
- Функции
- Интеграция встроенного программного обеспечения
- Начните здесь
- Программирование на C
- Программирование на языке ассемблера MPASM ™
- MPLAB® Harmony v3
- Начните здесь
- Библиотеки MPLAB® Harmony
- MPLAB® Harmony Configurator (MHC)
- Проекты и учебные пособия MPLAB Harmony
- Периферийные библиотеки на SAM L10
- Начало работы с Периферийными библиотеками Harmony v3
- Периферийные библиотеки с низким энергопотреблением на SAM L10
- Периферийные библиотеки на SAM C2x
- Начало работы с периферийными библиотеками Harmony v3
- Приложение с низким энергопотреблением с периферийными библиотеками Harmony v3
- Периферийные библиотеки на SAM D21
- Периферийные библиотеки на SAM D5x / E5x
- Начало работы с периферийными библиотеками Harmony v3
- Приложение с низким энергопотреблением с периферийными библиотеками Harmony v3
- Peripheral Libra
- Периферийные библиотеки на SAM L10
- Интеграция встроенного программного обеспечения
Planet Analog - Включите произведение коэффициента усиления на полосу пропускания операционного усилителя в уравнения рабочих характеристик активного фильтра нижних частот Рауха
Примечание редактора : Мой хороший друг и давний коллега Майкл Стеффес расширяет мою вводную статью «Основы фильтра Рауха» и добавляет некоторые очень полезные и практические идеи для дизайнеров о фильтре Рауха.
Переход от простой передаточной функции активного фильтра нижних частот с множественной обратной связью (MFB или Rauch), предполагающей идеальный усилитель с обратной связью по напряжению (VFA), к усилителю, включающему большее количество элементов операционного усилителя, может быть выполнен несколькими способами. Более ранний (2006 г.) проход в этом 1 сообщил о передаточной функции LP 3 -го порядка , где кубические коэффициенты на самом деле были немного ошибочными - они будут исправлены здесь. В недавнем обсуждении 2 цитируется источник 3 2005 года, в котором используемая модель усилителя не отражала полный операционный усилитель.Этот источник разработал 3 коэффициента порядка и , предполагая, что элементы обратной связи внешнего фильтра были подключены к тому, что группы разработчиков операционных усилителей называют узлом компенсации. Этот узел с высоким импедансом устанавливает коэффициент усиления постоянного тока без обратной связи и доминирующую полюсную частоту, но фактически находится за выходным каскадом, который управляет внешним миром с источником с более низким импедансом, буферизующим узел компенсации.
Включение выходного каскада в анализ MFB значительно упрощает результаты и приближает их к реальной реализации.Скорректированные коэффициенты для кубической схемы, разработанной в ссылке 1, будут показаны здесь, а затем использованы в примере проекта с очень медленным операционным усилителем для прогнозирования положения смещенных полюсов из-за произведения коэффициента усиления на ширину полосы операционного усилителя (GBW или GBP). Продолжение моделирования с тем же самым GBW в полной модели ОУ VFA покажет, насколько хорошо работает кубический прогноз.
Улучшение уравнений производительности MFB:
Исходя из идеальных уравнений операционного усилителя для конструкции MFB 4 , добавление простой однополюсной модели операционного усилителя с разомкнутым контуром изменит передаточную функцию до уровня нижних частот 3 -го порядка .Повторение шагов из ссылки 1, раздел 7, для схемы и нумерации RC на рисунке 1 даст передаточную функцию нижних частот 3-го порядка -го порядка без нулей.
Исправляя ошибки в ссылке 1, сначала смоделируйте операционный усилитель как однополюсную модель с коэффициентом усиления постоянного тока A или и доминирующей полюсной частотой ω a (не ω или , которая является целевой характеристической частотой фильтра). - повсюду работают в радианах. Продукт GBW для операционного усилителя будет A ol ω a /2 π.Для каждого термина старая форма (ссылка 1) и исправленный термин будут показаны вместе.
Разработка передаточной функции с этой моделью операционного усилителя для схемы на Рисунке 1 дает следующую форму (Ссылка 1):
Как указано в справке 1, можно (и часто очень полезно) включить емкость на землю на инвертирующем суммирующем переходе. Эта настройка C t представляет собой паразитный ОУ и / или специально добавленный внешний конденсатор для настройки запаса по фазе. Передаточная функция остается 3 -го порядка , включая C t , и уравнения коэффициентов становятся немного более сложными.Здесь будут показаны более простые формы без C t . Приведение кубики в моническую форму с B3 = 1 дает следующие исправленные выражения:
Хотя это, конечно, несколько сложно, на данном этапе легко создать электронную таблицу для расчета каждого из значений коэффициентов из решений RC и рассматриваемого операционного усилителя и создания рассчитанных положений полюсов с помощью кубического решателя. Это будет сделано здесь с намеренно очень медленным устройством, показывающим большой сдвиг в результирующей форме фильтра с обратной связью, предсказанной кубическим решением и скорректированными коэффициентами.Это более точное решение все еще игнорирует паразитную емкость операционного усилителя на инвертирующем входе, выходное сопротивление разомкнутого контура операционного усилителя и любые полюса более высокого порядка в отклике разомкнутого контура.
Тестирование уравнений производительности MFB, включая GBW
операционного усилителяЕсли перейти к примерам схем, показанным в ссылке 4, и выбрать операционный усилитель ближе к «требуемому» минимуму (3,9 МГц), инструмент ADI (ссылка 5) сообщает (при условии, что будет применена процедура настройки GBW), последние полюса будут довольно сдвинуты немного.Цели проектирования из ссылки 4 находятся здесь:
- Коэффициент усиления постоянного тока -10 В / В (20 дБ)
- Отклик на слабый сигнал, пик 1 дБ
- F -3 дБ = 100 кГц
Это дает нам целевые значения для активного фильтра с коэффициентом усиления -10 В / В и
4. F o = 80,62 кГц
5. Q = 0,957
Чтобы протестировать кубические решения с реальной симуляцией операционного усилителя, используйте GBW OPA377 5,4 МГц (ссылка 6). Эти 5,4 МГц получены в результате теста TINA (Reference 7) для частотной характеристики Aol и немного ниже заявленных 5.5Mhz для устройства.
Несколько решений RC были показаны в ссылке 4, где здесь в уравнении кубического коэффициента, показанном выше, будет использоваться самый низкий пиковый коэффициент усиления шума инструмента Intersil (ссылка 8). Эти значения RC показаны в таблице 1.
Таблица 1
Значения MFB RC из решения Intersil
Термины операционного усилителя OPA377 (ссылка 6) для использования в кубических коэффициентах показаны в таблице 2.
Таблица 2
Требуемые термины модели разомкнутого контура однополюсного ОУ
Результирующие значения коэффициентов для выражения кубического полюса показаны в таблице 3.
Таблица 3
Оценка кубического коэффициента
Кубический решатель возьмет их и вернет действительный полюс и комплексные пары полюсов, представленные в действительном и мнимом выражении в радианах. Их нужно настроить на Гц, а затем на формат F o и Q. В таблице 4 показаны те результаты, где значения F - и Q намного ниже целевого результата при использовании операционного усилителя с полосой пропускания 5,4 МГц.
Таблица 4
Кубическое решение для F o и Q.
Продолжая моделирование TINA с использованием модели OPA377, дает полученную форму частотной характеристики на рисунке 2:
Рисунок 2
Схема моделирования MFB с использованием модели OPA377 и значений Intersil RC.
А затем извлечение F o и Q из моделируемой характеристики усиления дает этот результат, включая полную модель операционного усилителя в таблице 5.
Таблица 5
Извлечение F o и Q из моделируемой формы отклика.
Кубическое решение предсказало замкнутый контур 2 nd полюс порядка F o = 73,1 кГц, тогда как полная симуляция показала 73,5 кГц. Он также предсказал Q = 0,919, тогда как полное моделирование показало 0,914. Очевидно, что приведенные здесь скорректированные коэффициенты очень хорошо учитывают произведение коэффициента усиления на полосу пропускания операционного усилителя и фиксируют большую часть сдвига полюсов, идущего к полной модели операционного усилителя в этом примере. Кроме того, результирующая ошибка соответствия цели очень велика, что позволяет предположить, что на этом этапе следует применить процедуру регулировки GBW, если к конструкции применяется такое медленное устройство.Инструмент ADI включает эту функцию в качестве опции, хотя в настоящее время кажется, что ни один из других онлайн-инструментов активного фильтра не реализует скорректированный поток проектирования для активного фильтра нижних частот Рауха.
Ссылки на разработку MFB LP Cubic.
- TI Application note «Методология проектирования фильтров MFB в приложениях интерфейса ADC», Майкл Стеффес, февраль 2006 г.
- Planet Analog, 28 января 2018 г., Стив Таранович, Основы фильтра Рауха
- Презентация университета, июнь 2005 г. «Аналоговый фильтр для телекоммуникаций», А.Баширотто, Статья
- EDN, «Тестирование инструментов операционных усилителей на точность конструкции активного фильтра и динамический диапазон», Майкл Штеффес, декабрь 2017 г.,
- Страница входа для интерактивного мастера активных фильтров Analog Devices. Требуется логин.
- TI, «Недорогой операционный усилитель CMOS с низким уровнем шума, 5,5 МГц» Симулятор
- TINA доступен от DesignSoft для
- Начальная страница онлайн-инструментов для проектирования операционных усилителей Intersil. Требуется логин.
Вычисления передаточной функции нижних частот RC
Вычисления передаточной функции нижних частот RC Роберт Кессель
Код 8123
Военно-морская исследовательская лаборатория
31 января 2000 г.
Аннотация
Входное и выходное напряжение RC-фильтра нижних частот может служить полезным тестом. случай обработки редукции данных поведенческой передаточной функции.Аналитический выражения существуют для всех этапов линейного анализа и, следовательно, составляют этот фильтр особенно полезен при отладке числового программного обеспечения.
Ключевые слова: анализ линейных систем, частотная область, переменный интервал. графики, ступенчатый переход, передаточная функция, отладка числового программного обеспечения.
RC-фильтр нижних частот в качестве тестового примера
для расчета поведенческой передаточной функции
W курица отладка числового программного обеспечения, очень хорошо иметь известную аналитическую прецедент.Для расчетов, требуемых линейным анализом установившегося состояния поведенческой динамики, RC-фильтр нижних частот может использоваться для обеспечения особенно удобный тестовый случай. Обработка для первой оценки поведенческого передаточная функция из данных подкрепления временных рядов и скорости отклика как а также использование передаточной функции для прогнозирования поведения показано на Рисунок 1. Тестовый пример просто заменяет поведенческие данные, появляющиеся на обеих фазах с соответствующим вводом и выходные пары от RC-фильтра нижних частот.
Рисунок 1 Схема A
представление алгоритма, используемого для первого извлечения передаточной функции
а затем, во-вторых, спрогнозируйте поведение по новому расписанию. Верхние левые изображения
проиллюстрируйте поведенческий выход на образец подкреплений. В середине слева
изображает преобразование этих данных в частоты и деление
вывод по вводу. Нижнее левое изображение представляет передаточную функцию.
Левая часть правой половины рисунка иллюстрирует расписание и его
представление в частотной области.Нижняя часть правой стороны
на рисунке показано, что данные умножаются на передаточную функцию для
производят частотное представление прогнозируемого поведения. Это
преобразован во временную область и по сравнению с фактическим поведением как
проиллюстрировано в верхней правой части рисунка.
Поскольку все числовые программы, используемые для генерации цифр для этого обсуждение написано в IDL, индекс массива для массива элементов n работает от 0 до n-1 .И FORTRAN, и MATLAB имеют массив индекс от 1 до n . Учтите это при портировании код. Следует также отметить, что несколько определений Фурье существует преобразование, которое может изменить нормализацию или преобразовать результаты к комплексно-сопряженному.
Запуск быстрого преобразования Фурье
Прежде чем пытаться что-либо сделать с линейным анализом, хорошо бы сначала покажите, что процедура быстрого преобразования Фурье (БПФ) работает. А стандартная процедура БПФ преобразует массив из 2 n чисел в другой массив из 2 n чисел, где n немного целое число. 1 Следует отметить два важных момента. Во-первых, все примеры в этом обсуждение будет иметь 256 элементов. секунд, шкала времени и частоты должны генерироваться независимо от процедуры БПФ.
В наиболее общем виде входные и выходные массивы в паре сложный. В данном случае, показанном на На рисунке 1 данные во временной области строго реальны. Выход БПФ при строго реальном вводе будет сложным, но будет также обладают свойством симметрии, называемым эрмитовым.Эрмитский комплекс массив имеет действительную часть отрицательной частотной составляющей, равную действительная часть положительной частотной составляющей и мнимая часть отрицательная частотная составляющая равна отрицательной мнимой части положительной частотной составляющей, или в виде пары выражений
а также где h (f) - комплексная функция частоты. Как хорошо. Какие действительно нужен тестовый пример только для процедуры БПФ, прежде чем работать над более общий тестовый пример RC-фильтра нижних частот. 2Поскольку входные данные тестового примера, которые будут следовать, используют прямоугольные импульсы, это имеет смысл только использовать прямоугольный импульс для проверки БПФ. На рисунке 2 показан элемент из 256 массив, где первые 32 элемента равны 1.0, а все остальные элементы - 0,0. Если временной интервал для 256 отсчетов составляет 2000 секунд, это соответствует спаду импульса в 250 секунд. Есть некоторые тонкости, связанные с тем, как точно преобразовать реальные аналоговые данные в это цифровое представление, которое будет рассмотрено ниже.А пока обратите внимание абсцисса этого графика - это просто номер индекса массива. Используя этот массив как вход, действительная и мнимая части, показанные на Рисунок 3 являются сложным выходом процедуры БПФ. Также показан комплекс сопрягать, что получается при использовании альтернативного определения Преобразования Фурье использовали Press, Flannery, Теукольский и Веттерлинг (1992). (Альтернативное определение было также используется в исходном коде сокращения данных на основе FORTRAN). Хотя оба действительная и мнимая части БПФ имеют симметрию, точная форма кажется не соответствует эрмитовой симметрии, заданной Уравнения 1 и 2.Явное отсутствие эрмитовского симметрия вызвана обернутой формой, используемой IDL и почти всеми другими Подпрограммы БПФ (Press et al. , 1992). Как развернуть выходной сигнал БПФ в частотной области будет рассмотрен ниже в контексте создание шкалы времени и частоты. Графики амплитуды и фазы для комплексного выходного массива БПФ показаны на Рисунок 4. Преобразование комплексного элемента массива БПФ к его соответствующей величине и фазе сделано как
а также Обратите внимание, что при использовании уравнения 4 в компьютерном коде необходимо включить соответствующую логику захвата для а также корпуса и установите f h (f) на правильное значение как исключения.Кроме того, компьютерный код должен возвращать правильный фаза, когда один или оба и меньше нуля, поэтому этот полный диапазон - р < f h (f) p используется.
Рисунок 2 Квадрат из 256 элементов
импульс как тестовый вход БПФ. Значения массива находятся в
one_sq_pulse.dat
и подпрограмма IDL, используемая для генерации как значений, так и графика,
fig_one_sq_pulse.pro
Рисунок 3 The
реальная часть (верхняя панель) и мнимая часть (нижняя панель) 256 элемента
Вывод БПФ.Также пунктирной линией показано комплексное сопряжение, которое
просто меняет знак мнимой части. Комплексное сопряжение
форма будет получена с помощью числовых рецептов БПФ.
Значения массива находятся в
one_sq_pulse_freq.dat
а процедура IDL, используемая для генерации как значений, так и графика, - это fig_one_sq_pulse_freq_v1.pro.
Рисунок 4 величина (верхняя панель) и фаза (нижняя панель) 256-элементного БПФ
выход. Процедура IDL, используемая для создания графика, выглядит следующим образом: fig_one_sq_pulse_freq_v2.про.
Еще один момент, который следует отметить перед тем, как перейти к тесту нижних частот RC. БПФ не вычисляет непрерывное преобразование Фурье. Для большинства частично различия незначительны и обычно ограничиваются эффектами наложения спектров. на более высоких частотах. Наложение - это процесс, в котором амплитуды от более высокочастотные компоненты ложно передаются на низкочастотные составляющие. Увидеть Press et al. (1992) для более длительного обсуждения и лежащей в основе математики.Для сингла импульс, данный
аналитическое преобразование Фурье, вычисленное с определением соответствия который используется БПФ IDL На рисунке 5 показана величина и фаза уравнения 6 оценивается при каждая из частот БПФ в Рисунок 4. 3 Хотя аналитическое выражение спадает быстрее, чем БПФ, кривые имеют по сути та же форма.
Рисунок 5 The
величина (верхняя панель) и фаза (нижняя панель) аналитического Фурье
преобразование прямоугольного импульса. График нормализован, поэтому компонент постоянного тока
Реальная часть - 1.0. Значения массива находятся в
one_sq_pul_freq_ana.dat
и подпрограмма IDL, используемая для генерации как значений, так и графика, fig_one_sq_pul_freq_v2_ana.pro.
Пара входа и выхода ФНЧ фазы измерения
Рассматривая пару прямоугольных импульсов в качестве входа для фильтра нижних частот, простые аналитические выражения будут существовать как для ввода, так и для вывода. Выражение для ввода
Рекомендуется, чтобы границы импульсов совпадали с временными интервалами, используемыми для Пример уравнения 7.С тех пор будет 256 ячеек за 2000 секунд испытания, эти границы имеют интервал D = 2000/256 или 7,81250 секунд. За эта фаза измерения:| т 1 = | 218,750 |
| т 2 = | 414.062 |
| т 3 = | 656,250 |
| т 4 = | 796,875 |
Рисунок 6 Выход RC
фильтр нижних частот (верхняя панель), который будет генерироваться из двухимпульсного входа
(нижняя панель).Значения t, V из (t) и
V в массивах (t) находятся в
two_pulse.dat
и подпрограммы IDL, используемые для генерации значений:
make_r_of_t.pro и
make_lo_pass_b_of_t_v4.pro. Процедура IDL, используемая для создания графика, выглядит следующим образом:
plot_input_output.pro.
Есть три аналитических свойства и один числовой аспект Уравнение 8, которое необходимо иметь в виду. Во-первых, это что-то вроде приближения, поскольку большинство способов построения и измерение такой схемы будет включать уровень постоянного тока в установившемся состоянии.При условии импульсы находятся в первой половине испытания и t равно остается достаточно маленьким, V из (t) будет эффективно возвращено к нулю к концу 2000-секундного испытания, и можно игнорировать уровень постоянного тока. Во-вторых, напряжение, достигнутое к концу импульса, должно использоваться как стартовое. напряжение для спада в следующем интервале. В-третьих, каждый импульс затухает независимо. Следовательно, к пятому интервалу выражение становится немного длиннее. Оценка уравнения 8 при наборе 256 дискретных образцы времени довольно важны.Рисунок 7 показывает взаимосвязь между V в (t) , В, , из (t) , и интервалы времени около переднего фронта первого импульса. Входной сигнал можно легко и почти идеально смоделировать плоской дискретной линией. сегментов, поскольку фронты нарастания и спада импульса были выбраны в соответствии с временем границы бункера. Уравнение 8, с другой стороны, кривые во всем интервале времени. После попытки среднего значения и выборка моментальных снимков приближается, по крайней мере, в этом случае, к средней выборке имеет лучшую производительность.
Рисунок 7 V дюйм (т) и V out (t) наложено на интервалы времени около первого импульса
поднимающийся край. Пунктирные линии показывают среднее значение выборки, используемое для В вых (т)
Преобразование в частотную область с помощью БПФ
Имея в руках пару входов и выходов тестового примера, было бы удобно использовать БПФ. для численного преобразования данных, показанных в Рисунок 6 в частотной области.БПФ IDL предполагает, что прямое преобразование Фурье
где h (f) - функция в частотной области, эквивалентная функции времени H (т) . Press et al. (1992) определение для преобразование Фурье комплексно сопряжено с Уравнение 9 дается формулой Используется определение уравнения 10 в версии FORTRAN программы обработки данных (Паля и др. , 1996, 2000). На рисунке 8 показаны реальные и мнимые части v в (f) , которые возникают, когда IDL FFT запустить на массиве 256 образцов, созданном из Уравнение 7.На рисунке 9 показано реальное и мнимые части v из (f) , которые возникают, когда IDL FFT выполняется на массиве из 256 отсчетов, сгенерированном на выходе RC-фильтра нижних частот как задается уравнением 8. RC Выходной сигнал нижних частот значительно больше нуля только для низких частот. Как и ожидалось, высокочастотные составляющие близки к нулю.
Рисунок 8 Реальная часть
(верхняя панель) и мнимая часть (нижняя панель) для теста с двумя прямоугольными импульсами
вход преобразован в частотную область с помощью БПФ.Значения массива
находятся в
two_sq_pulse_freq.dat и
подпрограмма IDL, используемая для генерации как значений, так и графика, fig_two_sq_pulse_freq_v1.pro.
Фиг.9 Реальная часть
(верхняя панель) и мнимая часть (нижняя панель) для выхода RC-фильтров нижних частот
из двух прямоугольных импульсов, преобразованных в частотную область с помощью БПФ. Ценности
массива находятся в
two_rou_pulse_freq.dat
и подпрограмма IDL, используемая для генерации как значений, так и графика, fig_two_rou_pulse_freq_v1.про.
Построение преобразований Фурье
Если вы привыкли с ними работать, обернутый частотный диапазон Форма, используемая большинством подпрограмм БПФ, достаточно естественна. Тем не менее приятно развернуть и иногда отображать массивы как функцию частоты. Мы возьмем небольшое отступление от шагов, изложенных в На рис. 1 показано, как распаковка сделано. Масштабирование частоты БПФ необходимо сначала создать, чтобы сюжеты.
Шкала частот для БПФ определяется периодом времени между для последовательных выборок и общий временной интервал для выборки.в В настоящем деле этот общий временной интервал составляет испытательный срок. Самый низкий ненулевой частотная составляющая
Наивысшая частотная составляющая задается критической частотой Найквиста, данный где D - период времени между последовательными образцы. Частотные составляющие между f 1 и f c - это просто целые числа, кратные f 1 :
| ||||||||
Таблица 1 Индексы массива и
соответствующие частоты, выдаваемые IDL FFT в свернутой форме
| индекс | 0 | 1 | 2 | ... | 126 | 127 | 128 | 129 | ... | 255 |
| частота | 0 | f 1 | f 2 | ... | ( f c -2 f 1 ) | ( f c - f 1 ) | f c | - ( f c - f 1 ) | ... | ф -1 |
| (в мГц) | 0.0 | 0,5 | 1,0 | ... | 63,0 | 63,4 | 64,0 | -63,5 | ... | -0,5 |
Разворачивая структуру таблицы 1, БПФ в порядке увеличения частоты включает в себя замену двух половинки массива. Рисунок 10 показывает два развернутых прямоугольных импульсных входа в виде графиков действительной и мнимой частей. Эрмитовы симметрии, заданные Уравнения 1 и 2 хорошо видно. Рисунок 11 и На рисунке 12 показаны величина и фазовые диаграммы для двухимпульсного входа и выхода RC-фильтра нижних частот.
Рисунок 10 Реальная часть
(верхняя панель) и мнимая часть (нижняя панель) для входа двух прямоугольных импульсов
преобразованы в частотную область с помощью БПФ, а затем развернуты в
частота. Значения f и v в массивах (f) находятся в
two_sq_pulse_freq_v2.dat
и подпрограмма IDL, используемая для генерации как значений, так и графика,
fig_two_sq_pulse_freq_v2.pro.
Рис.11 амплитуда (верхняя панель) и фаза (нижняя панель) для двух прямоугольных импульсов
входной сигнал преобразован в частотную область с помощью БПФ, а затем развернут в
частота.Процедура IDL, используемая для создания графика, выглядит следующим образом: fig_two_sq_pulse_freq_v3.pro.
Рисунок 12 амплитуда (верхняя панель) и фаза (нижняя панель) для RC-фильтров нижних частот
выход из двух прямоугольных импульсов, преобразованных в частотную область с
БПФ. Значения массивов f и v out (f) находятся в two_rou_pulse_freq_v2.dat и процедура IDL, используемая для генерации
как значения, так и график fig_two_rou_pulse_freq_v2.pro.
Вычислить числовую передаточную функцию
Простейшая оценка передаточной функции делением двух БПФ использует выражение
Для теста низких частот RC, выходное напряжение, v out ( f ), занимает место b ( f ) и аналогично входное напряжение, v в ( f ), заменяет r ( f ) в Уравнение 18, дающее численную оценку для передаточная функция нижних частот RC, заданная как Поскольку v из ( f ) и v из ( f ) являются сложными, в компьютерной программе, оценивающей Уравнение 19.Рисунок 13 и Рисунок 14 показать передаточную функцию, полученную с помощью Уравнение 19 как действительное, так и мнимое пары частей или величин и фазовых графиков в развернутой форме.
Рисунок 13 Реальная часть
(верхняя панель) и мнимая часть (нижняя панель) для передаточной функции
развернутый по частоте. Обернутый БПФ массив только передаточной функции
в
num_t_fun_freq_v1.dat.
Значения f и g RC, номер ( f ) в развернутом виде
массивы находятся в
num_t_fun_freq_v2.Дат
и подпрограмма IDL, используемая для генерации как значений, так и графика, fig_num_t_fun_freq_v1.pro.
Рисунок 14 Величина
(верхняя панель) и фаза (нижняя панель) для передаточной функции, развернутой в
частота. Процедура IDL, используемая для создания графика, выглядит следующим образом: fig_num_t_fun_freq_v2.pro.
Вычислить аналитическую передаточную функцию
Аналитическое выражение для передаточной функции RC-фильтра нижних частот:
где фазовый угол а критическая частота фильтра, f o , является характеристикой фильтр, связанный с его постоянной времени, t = RC, соотношением Уравнение 20 - это комплексный сопряжение выражения в Паля и др., (1996) соответствующий переключателю в определении преобразования Фурье. Рисунок 15 - величина и фазовые графики из прямой оценки g RC ( f ). Рисунок 14 полностью соответствует с рисунком 15.
Рисунок 15 Величина
(верхняя панель) и фаза (нижняя панель) для передаточной функции, развернутой в
частота. Обернутый БПФ только массив передаточной функции находится в
ana_t_fun_freq_v1.dat.
Значения f и g RC ( f ) в развернутом виде
массивы находятся в
ana_t_fun_freq_v2.Дат и
подпрограмма IDL, используемая для генерации как значений, так и графика, fig_ana_t_fun_freq_v2.pro.
При разработке процедур ILD возникла довольно интересная трудность. которые имеют ожидаемое близкое согласие между Рисунок 14 и Рисунок 15. В начальные версии двух тестовых пар входных / выходных импульсов, восходящий и нисходящий края имели разные временные отношения. Выход эффективно отставал вход для переднего фронта, но ведущий вход для заднего фронта. Этот вид процесса не поддается описанию в рамках линейного анализа, который предполагает одинаковые временные отношения на обоих краях.Этот аспект обработка, вероятно, подлежит дальнейшему изучению, поскольку численная оценка для передаточной функции нижних частот RC с этим временным соотношением несоответствие выглядело более чем напоминанием тех, что видели с поведенческие данные. Возможно, птицы используют два разных процесса при адаптации к возрастающей и падающей норме подкрепления.
Тестовая фаза входной и выходной пары нижних частот
В качестве тестовой фазы предсказания линейного анализа рассмотрим три импульсный вход. Аналитическая форма, аналогичная Уравнение 7 для входа
Выражение для выхода RC-фильтра нижних частот с учетом трех прямоугольный импульсный вход Для фазы тестирования снова полезно выбрать совпадающие фронты импульсов. границы временного интервала:| т 1 = | 125.000 |
| т 2 = | 195,312 |
| т 3 = | 289,062 |
| т 4 = | 359,375 |
| т 5 = | 539,062 |
| т 6 = | 695,312 |
Рисунок 16 Выход RC
фильтр нижних частот V out (t) (верхняя панель), который будет генерироваться из
трехимпульсный вход V в (t) (нижняя панель). Также нанесено на верхнюю панель,
хотя почти невозможно различить в масштабе этого графика, является ли линейный прогноз
V из до (t). Ценности
т, V из (т), V в (т) и
V out pred (t) массивы находятся в
three_pulse.dat. Процедуры IDL
используются для генерации аналитических значений фазы тестирования:
make_r_of_t.про и make_lo_pass_b_of_t_v5.pro. Линейное прогнозирование выполняется с помощью
IDL-подпрограмма linear_predict.pro.
Процедура IDL, используемая для создания графика, выглядит следующим образом: plot_input_output_v2.pro.
Вычислить линейное предсказание
Прогнозирование выхода RC-фильтра нижних частот на основе числового оценка передаточной функции в Рисунок 1 с трехимпульсным входом: просто. Просто следует по шагам показано в правой части рисунка 1. Графики частотной области, полученные как промежуточные результаты прогноза очень похожи на полученные при оценке передаточной функции.Следовательно, эти участки не включены.
Прогнозирование требует трех шагов. Во-первых, входной прямоугольный импульс данные преобразуются в частотную область с помощью БПФ. Тогда один использует выражение для линейного предсказания в частотной области данный
где b ( f ), g ( f ) и r ( f ) - преобразования Фурье B (t), G (t-t) и R (t) соответственно. Подставив в соответствующие функции для ФНЧ RC фильтр выражение становится Как и в случае оценки передаточной функции, оценка Уравнение 26 выполнено с комплексным арифметика.Остается только обратное преобразование v из до ( f ) во временную область. IDL определение обратного или обратного БПФ Обратите внимание, что процедура IDL FFT также автоматически обрабатывает нормализацию обратное преобразование. По сравнению, (Press et al. , 1992) определяют спину преобразовать как и пользователь несет ответственность за правильную настройку нормализации. Предсказание результат этих трех шагов показан на Рисунок 16.Сравнить результаты качественно
Качественное сравнение линейного предсказания и аналитического выражение просто вопрос взгляда на две кривые.В качестве как показано на рисунке 16, линейная предсказание почти неотличимо от аналитического выражения, данного Уравнение 24. Остатки график на рисунке 17 показывает, что прогноз с точностью до машинной шкалы точности.
Рисунок 17 Остаток для
линейное предсказание V out pred (t) - V out (t)
как функция времени. Процедура IDL, используемая для создания графика, выглядит следующим образом:
plot_output_diff.pro.
Сравнить результаты количественно
При отсутствии установленной причины поступить иначе, приведенная сумма хи-квадрат квадраты расхождений - стандартный метод ответа на этот вопрос (Бевингтон, 1969).Следующий Бевингтон (1969), а также Паля и др. (1996), c n 2 за расхождение между измеренными скорость ответа B (t) и прогнозируемая скорость ответа B pred (t) - это
где n - разница между количеством данных точек N и количество настраиваемых параметров n и s 2 B i есть отклонение измеренной скорости отклика i th B (т и ).Так как у прогнозов нет свободных параметров, n = 0, коэффициент нормализации упрощается, как показано, до 1/ N и n = N .Поскольку тестовый пример RC low pass полностью представляет собой численное упражнение, здесь нет набор s 2 V out pred , i значений использовать с уравнением 29 или 30. Конечно, можно бесплатно вычислить равновзвешенный в п 2 . Помимо количественного подтверждения того, что прогноз в масштабе машинной точности такое упражнение мало что даст.Набор s 2 V out pred , i значения могут генерироваться независимо, а затем варьироваться, чтобы понять, как вероятности зависят от верности линейного предсказания аналитическому выражение.
Список литературы
Бевингтон, П. Р. (1969). Сокращение данных и анализ ошибок для физических наук (стр. 187-203). Нью-Йорк: Книжная компания McGraw-Hill.
Паля, У.Л., Вальтер, Д., Кессель, Р., и Лакк Р. (1996). Исследование динамического поведения с фиксированным расписанием исчезновения и линейный анализ. Журнал экспериментального анализа Поведение , 66 , 391-409.
Паля У.Л., Уолтер Д., Кессель Р. и Лаке, Р. (1999). Линейное моделирование устойчивой динамики поведения. В печати на Журнал экспериментального анализа поведения .
Press, W.H., Flannery, B.P., Teukolsky, S.A. и Феттерлинг, W.T.(1992). Числовые рецепты в FORTRAN 77: The Art of Scientific Computing, 2 nd (стр. 490-602). Кембридж: Издательство Кембриджского университета.
Сноски:
1 Существуют более специализированные пакеты БПФ, которые обрабатывают массивы любой длины.
2 дюйм другими словами, предварительный тестовый пример перед тестовым примером. К счастью, последовательность обрезается Вот. Предварительный тестовый пример перед предварительным тестовым набором не требуется.
3 Хорошо, использование уравнения 6 действительно кажется быть пре-пре-тестовым случаем, но на этом последовательность действительно заканчивается.В самом деле. 😉
Файл переведен с L A T E X от T T H, версия 2.21.
24 мая 2000 г., 15:26.
(с более поздними ручными модификациями уравнений, фигура крест ссылки и тому подобное)
Присылайте комментарии / критику / предположения по адресу
Дата последней редакции: 19 августа 2002 г.
Хотите простора и ясности в ваших миксах? Используйте фильтры нижних частот • Почему правила Logic Pro
Онлайн-обучающие программы по High Passing в наши дни примерно так же распространены, как и видео про кошек.
Это настолько распространено, что о нем почти не стоит говорить! Если вам нужно пространство и четкость, очистите свои дорожки с помощью фильтров высоких частот .
Но установка фильтров высоких частот - это не совсем наука, не так ли?
Сколько это уже много? И не всегда ли сложно найти идеальную частоту для настройки фильтров?
Есть такой , более простой способ сделать всю эту штуку с фильтром высоких частот. Но вы должны посмотреть на другой конец спектра…
И это с Low Pass .
Запутались? Разрешите пояснить:
Hi Pass Filters: Пылесос Audio’s
Фильтры высоких частот подобны пылесосам в мире аудио. Вы используете высокие передачи, чтобы расчистить свои дорожки.
Чаще всего ваш трек будет иметь низкий уровень шума. Вы не можете этого слышать, но он там:
Этот шум может быть слишком тихим, чтобы его можно было заметить. Но на самом деле это лишает вас запаса прочности и ясности!
За исключением бас-барабана или бас-гитары, большинству ваших треков не нужен звук в более низком диапазоне.Этот звук часто исходит из окружающего шума. Например:
- Кондиционер
- Музыкант двигается или натыкается на предметы
- Сосед косит газон
Подумайте о пыли в вашем доме. Это не так уж плохо, правда? Конечно, есть небольшая пыль, но ничего тоже плохо.
А теперь попробуйте собрать пылесосом всю пыль в вашем доме. Давай, пропылесось все это место - я подожду.
Сумка начинает наполняться, не так ли?
Этот низкий уровень шума подобен пыли в вашем доме.На одном треке все не так уж плохо. Но через 50 треков? Теперь ваш микс начинает выглядеть грязным .
И эта «грязь» коварно крадет четкость и пространство ваших миксов.
Недостатки высоких частот
Так что, если вы хотите простора и ясности, вам нужен высокий проход.
Но процедура высокого прохода всегда была немного обидчивой.
Правило всегда было:
- Перетащите фильтр высоких частот вверх, пока не услышите, что трек начинает звучать тонко, а затем
- Немного отключите фильтр, пока дорожка не перестанет звучать тонкой
В этом есть смысл, не так ли?
Вы хотите удалить все, что ниже определенной частоты.Но вы не хотите отбрасывать важные основные частоты ваших треков.
Вот проблема с настройкой фильтров верхних частот следующим образом:
Шум, который вы пытаетесь отключить, очень низкий. Настолько тихо, что даже не слышно.
Даже если в вашей системе есть что-то вроде сабвуфера, это может быть сложно услышать.
Я имею в виду, разве вечная борьба не всегда заставляет вашу басу или бас прорезать ваш микс?
Таким образом, очевидно, что будет сложно набрать что-то , которое вы на самом деле не слышите .
И если задуматься еще немного:
Вот почему фильтры низких частот - ваш лучший друг для высоких частот.
Низкий путь к успеху
Средние и высокие частоты всегда было легче услышать, чем низкие частоты. В то время как низкие частоты обычно больше «ощущаются», чем слышны.
Если бы только вы могли убрать средние и высокие частоты, низкие частоты было бы намного легче слышать!
Ну-ну-ну. Фильтр низких частот может сделать именно это - удалить средние и высокие частоты.
А что останется, когда пропадут средние и высокие частоты?
Все, детка.
Так что процедуру высокого прохода действительно нужно полностью изменить:
- Перетаскивайте фильтр нижних частот, пока не услышите только уродливый ненужный шум
- Когда вы выбираете частоту, запишите ее .
- Теперь обойдите ваш фильтр нижних частот, а
- Установите эту частоту фильтра верхних частот .
Вуаля! Теперь вы можете хирургическим путем удалять пыль и грязь из смесей.
Вам не нужно было гадать и шарить. Вы смогли найти , именно там, где он живет, .
Помимо шума
Эта тактика низких частот подходит не только для игроков низкого уровня. Фактически, это может помочь вам по-настоящему точно настроить низкие частоты ваших треков.
Иногда гитары, клавишные и другие инструменты могут иметь сбои, которые не нужны.
Гитарные усилителимогут иметь резонансы низких частот, которые звучат так, будто кто-то говорит через подушку, вместо мясистых гитарных тонов.
Клавишимогут издавать щелчки, механические шумы и другие ненужные звуки.
Когда вы проходите мимо, вы можете иметь гораздо более четкую картину того, что там происходит.
Так что, если низкие частоты гитары - это просто приглушенные резонансы - вперед! Вырежьте это сразу. Даже если это проникает в реальный тон инструмента. В любом случае, этот хлам тебе не нужен.
Заключение
Фильтры верхних частот имеют решающее значение для очистки ваших смесей для получения максимального пространства и прозрачности.Чем больше плагинов вы добавите в свои миксы, тем больше пользы от высокой проходимости проявятся.
Но критически подходить к High Pass - это все равно что пытаться найти что-нибудь в темноте.
Да, вы можете догадаться, что, по вашему мнению, вы слышите. Но почему бы не быть уверенным?
Используя низкие частоты, вы удаляете отвлекающие средние и высокие частоты и можете выполнить некоторую реальную работу.
Хотите узнать, как получить максимальную отдачу от EQ?
Я собрал бесплатных мини-курсов из 5 стратегий эквалайзера , которые я разработал на основе года записи и сведения.
Эти 5 стратегий изменили правила моего микширования. И они могут для вас тоже.

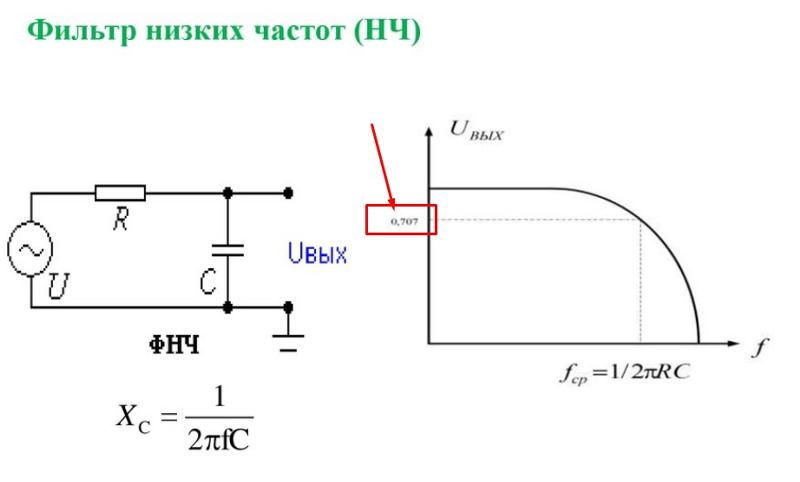 Как правило, средним значением является 4 Ом;
Как правило, средним значением является 4 Ом;